WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Eigenwaarden van vierkante matrices met de Ti83

Kan je eigenwaarden berekenen m.b.v. het
GRM CASIO Graph 100 of eventueel met TI 83 Plus(Silver)?
En hoe moet dat dan?
Bedankt voor de moeite
Florence
Poisma
Ouder - dinsdag 23 december 2003

Antwoord

De Ti83 heeft geen ingebouwde mogelijkheid om de eigenwaarden van een vierkante matrix uit te rekenen.
Maar niet getreurd, met een beetje nadenken is het toch mogelijk om de eigenwaarden van een vierkante matrix met de TI83 numeriek te benaderen.

De theorie achter de methode die hieronder volgt is de volgende:
Je kunt de eigenwaarden l van een vierkante n bij n matrix A berekenen door te stellen dat det(A-lI)=0 moet zijn. (Hierbij is I de eenheidsmatrix).
Dit levert een n-de graadsvergelijking in l op.
De oplossingen van deze vergelijking zijn de eigenwaarden.
Stel we hebben de matrix

De bijbehorende vergelijking wordt dan (6-l)(6-l)-1=0. De opossingen van deze vergelijking zijn l=5 en l=7.

Nu de TI-83:
Kies in het matrix menu EDIT

Voer nu de matrix in

Ga nu naar het Y=-scherm en voer bij Y1 in
Y1=det([A]-X*identity(2))
(det en identity haal je uit het matrix-Math menu. [A] krijg je door in het Matrix-Names menu de matrix A op te roepen.
Die 2 bij identity(2) slaat er op dat je een 2 bij 2 matrix hebt. Zonodig aanpassen als je matrix een andere dimensie heeft.

Plot nu de grafiek van Y1. (Graph)
In dit geval krijg je een parabool te zien: je hebt immers een tweede graads vergelijking.
De nulpunten van deze grafiek zijn de eigenwaarden die je zoekt.

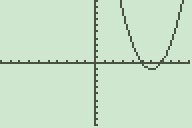
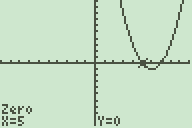
De nulpunten van deze grafiek kun je vinden met 2nd-Calc Zero

Antwoord geven de op de prompts van deze numerieke methode levert je achtereenvolgens de nulpunten en dus de eigenwaarden.

Over een methode op de Casio wordt bij ons nog nagedacht.
Als we daar een oplossing voor hebben hoor je nader!

Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 25 december 2003