WisFaq!

Loading jsMath...

De digitale vraagbaak voor het wiskundeonderwijs

HOME

\require{AMSmath}

Poolvergelijking

Hoe kan ik bepalen in welke punten de kromme gegeven in poolvergelijking r= 1+ cosq horizontale of vertikale raaklijnen heeft?

Ik snap dat je de afgeleide moet berekenen en dat je dan moet kijken voor welke waarden van q de teller en noemer 0 worden. Maar hier zit mijn probleem: hoe los ik zo'n goniometrische vergelijking op?

bedankt
jos
jos
Student Hoger Onderwijs België - zondag 30 november 2003

Antwoord

Een plaatje voor de duidelijkheid:

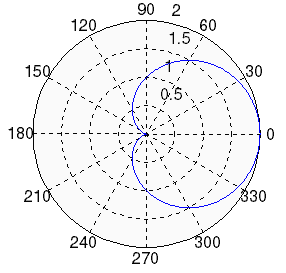
Als het goed is, heb je de volgende vergelijkingen gekregen:
voor de horizontale raaklijnen dx/dq = 0:
cos(q) + cos²(q) - sin²(q) = 0
ofwel
cos(q) + cos(2q) = 0
cos(q) = -cos(2q)
cos(q) = cos(p - 2q)
q = p - 2q (mod 2p) of q = -p + 2q (mod 2p)
3q = p (mod 2p) of q = p (mod 2p)
Dus op het interval [0, 2p) levert dit:
p/3, p, 5p/3

voor de verticale raaklijnen dy/dq = 0:
-sin(q) - 2·sin(q)·cos(q) = 0
ofwel
sin(q)(1 + 2·cos(q)) = 0
dit levert als oplossing (uitwerking moet lukken toch?):
0, p, 2p, 2p/3, 4p/3
Voor de waarde van q waarvoor beide afgeleiden 0 zijn (namelijk q = p), geldt iets bijzonders.
Voor dit punt moet de limiet bekeken worden van dy/dx.
Met behulp van de stelling van de l'Hôpital kun je zien dat hier 0 uit komt, dus in dit punt is de raaklijn horizontaal.
Dit alles in overeenstemming met de grafiek.
groet,

Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 1 december 2003