WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Parametervergelijking

gegeven een fct met parametervergelijking: x=t²-1 en y= t³-t

HOe kan ik op deze kromme de punten bepalen waar de raaklijn horizontaal en vertikaal is?

bedankt
jos
Jos
Student Hoger Onderwijs België - dinsdag 18 november 2003

Antwoord

Je kan dx/dt en dy/dt berekenen.
De punten waar de raaklijn horizontaal is corresponderen met de t waarden uit de vergelijking dy/dx=0.
De punten waar de raaklijn verticaal is corresponderen met de t waarden uit de vergelijking dx/dy=0.

dx/dt = 2t
dy/dt = 3t²-1
= dy/dx = (dy/dt)/(dx/dt) = (3t²-1)/(2t) = 0
= t = 1/3Ö(3) of t = -1/3Ö(3)

Vul je deze waarden in in de parametervoorstelling dan komt er voor elke t waarde een punt uit... Dit zijn de punten waar de raaklijn horizontaal is.

Je kan nu zelf hetzelfde doen voor de verticale raaklijn(en).

dx/dy= ...?

figuur: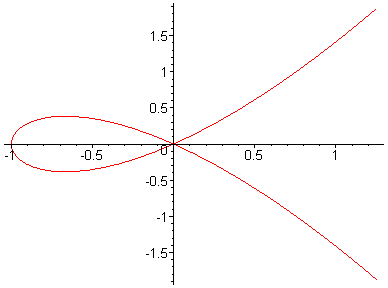

Koen Mahieu

Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 18 november 2003