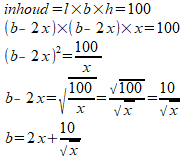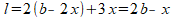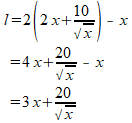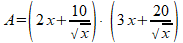|
|
|
\require{AMSmath}


Re: Dozen met vaste inhoud
Dankuwel, dit is nu duidelijker. Zou u mij willen uitleggen hoe ze komen op deze twee formules tussen haakjes? Ik snap niet waar ze deze vandaan hebben gehaald, en dan specifiek de tweede formule (als ik het goed zeg) tussen haakjes.
A
Leerling bovenbouw havo-vwo - dinsdag 13 februari 2024
Antwoord
Het gaat om deze opgave:

De breedte van het karton is b. Langs de lange zijde worden twee stroken met breedte x omhoog gevouwen voor de opstaande zijkanten, dan blijft voor de breedte van de doos over:
breedte doos = b-2x
De doos is vierkant, dus geldt ook:
lengte doos = b-2x
De hoogte wordt x. Gegeven is: de inhoud is 100. Met de formule voor inhoud kunnen we dan b uitdrukken in x:
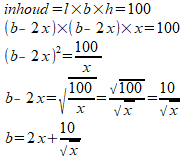
In figuur 11 van de opgaven zie je dat de lengte l van het karton twee keer de lengte van de doos is, plus drie keer de hoogte x:
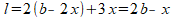
Vul de gevonden uitdrukking voor b in deze formule in:
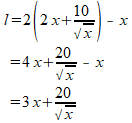
De oppervlakte A van het karton is breedte $\times $ lengte, ofwel b $\times $ l:
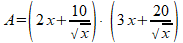
Hiermee is de formule gevonden waar je naar vroeg.
Is hiermee het probleem opgelost?

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 14 februari 2024
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|







 Dit is een reactie op vraag 98069
Dit is een reactie op vraag 98069