|
|
|
\require{AMSmath}



Re: Integraal met substitutie of niet
Goede avond Jan en KP,
De uitleg van KP ligt een beetje moeilijk en graag nog wat uitleg. Andere oefening (tweede)zonder problemen opgelost.
Goede nacht
Rik
Rik Le
Iets anders - zaterdag 2 april 2022
Antwoord
We beginnen met
$$\int\frac1{x\sqrt{x^2+x+1}}\,\mathrm{d}x
$$De eerste stap is kwadraat afsplitsen in $x^2+x+1$; dat wordt $\eqalign{(x+\frac12)^2+\frac34}$.
Vervang $\eqalign{x+\frac12}$ door $y$:
$$\int\frac1{(y-\frac12)\sqrt{y^2+\frac34}}\,\mathrm{d}y
$$Je kunt de wortel iets mooier maken door $\eqalign{y=\frac{\sqrt3}{2}z}$ te nemen: dan $\eqalign{y^2+\frac34=\frac34z^2+\frac34=\frac34(z^2+1)}$; er komt
$$\int\frac1{\frac{z\sqrt3-1}2\cdot\frac{\sqrt3}2\cdot\sqrt{z^2+1}}
\frac{\sqrt3}2\,\mathrm{d}z
=\int\frac2{z\sqrt3-1}\cdot\frac1{\sqrt{z^2+1}}\,\mathrm{d}z
$$Nu bekijken we deze driehoek:
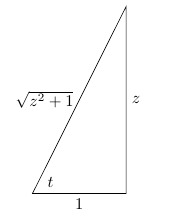
We substitueren $z=\tan t$.
Dan krijgen we ook $\eqalign{\frac1{\sqrt{z^2+1}}=\cos t}$ en $\eqalign{\mathrm{d}z=\frac1{\cos^2t}\,\mathrm{d}t}$.
Er komt
$$\int\frac2{\sqrt3\tan t-1}\cdot\cos t\cdot\frac1{\cos^2t}\,\mathrm{d}t
=\int\frac2{\sqrt3\sin t-\cos t}\,\mathrm{d}t
$$Voor dit soort integralen is $u=\tan\frac12t$ een veelgebruikte substitutie.
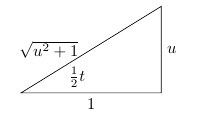
Nu krijgen we $\eqalign{\sin\frac12t=\frac u{\sqrt{u^2+1}}}$ en $\eqalign{\cos\frac12t=\frac1{\sqrt{u^2+1}}}$ en door de verdubbelingsformules vinden we
$$\sin t=\frac{2u}{u^2+1},\qquad
\cos t=\frac{1-u^2}{1+u^2}, \quad\text{ en }\quad
\tan t=\frac{2u}{1-u^2}
$$Met $t=2\arctan u$ komt er uiteindelijk
$$\int \frac2{\frac{2\sqrt3u}{1+u^2}-\frac{1-u^2}{1+u^2}}\cdot
\frac2{1+u^2}\,\mathrm{d}u=
\int \frac4{u^2+2\sqrt3u-1}\,\mathrm{d}u
$$De noemer kunnen we ontbinden als $(u+\sqrt3-2)(u+\sqrt3+2)$ en daarmee kunnen we de integraal schrijven als:
$$\int \frac1{u+\sqrt3-2}-\frac1{u+\sqrt3+2}\,\mathrm{d}u
$$De primitieve wordt dus
$$\ln(u+\sqrt3-2)-\ln(u+\sqrt3+2)
$$of
$$\ln\left(\frac{u+\sqrt3-2}{u+\sqrt3+2}\right)
$$Nu terugwerken.
Merk op dat we hebben gezien dat $\eqalign{z=\tan t=\frac{2u}{1-u^2}}$, hiermee kunnen we $u$ in $z$ uitdrukken: we lossen
$$zu^2+2u-z=0 \text{ of } u^2+\frac2zu-1=0
$$op: kwadraat afsplitsen geeft
$$\left(u+\frac1z\right)^2-\frac{z^2+1}{z^2}=0
$$en dus
$$u=-\frac1z\pm\frac1z\sqrt{z^2+1}
$$Omdat $u$ en $z$ hetzelfde teken moeten hebben nemen we
$$u=\frac1z\bigl(\sqrt{z^2+1}-1\bigr)
$$Nu nog netjes $\eqalign{z=\frac2{\sqrt3}(x+\frac12)}$ invullen en uitwerken.
NB we hadden de substituties $z=\tan t$ en $u=\tan\frac12t$ in een keer kunnen doen, met behulp van $\eqalign{z=\frac{2u}{1-u^2}}$ en $\eqalign{u=\frac1z\bigl(\sqrt{z^2+1}-1\bigr)}$, maar dat is wat onoverzichtelijker. Het zou wel een goede oefening in netjes werken zijn.
kphart
|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 4 april 2022
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2025 WisFaq - versie 3
|








 Dit is een reactie op vraag 93507
Dit is een reactie op vraag 93507 

