|
|
|
\require{AMSmath}



Re: Re: Zwaartelijnen in driehoek
Ik heb nog eens gekeken naar dit vraagstuk en heb een oplossing kunnen vinden m.b.v. analytische meetkunde. Deze oplossing is ietwat omslachtig, maar het is gelukt. Mogelijk vind ik misschien nog wel een oplossing met de "gewone vlakke meetkunde". Ik zie nog wel. Nogmaals bedankt.
J. Vri
Iets anders - zaterdag 24 juli 2021
Antwoord
Hier is een plaatje
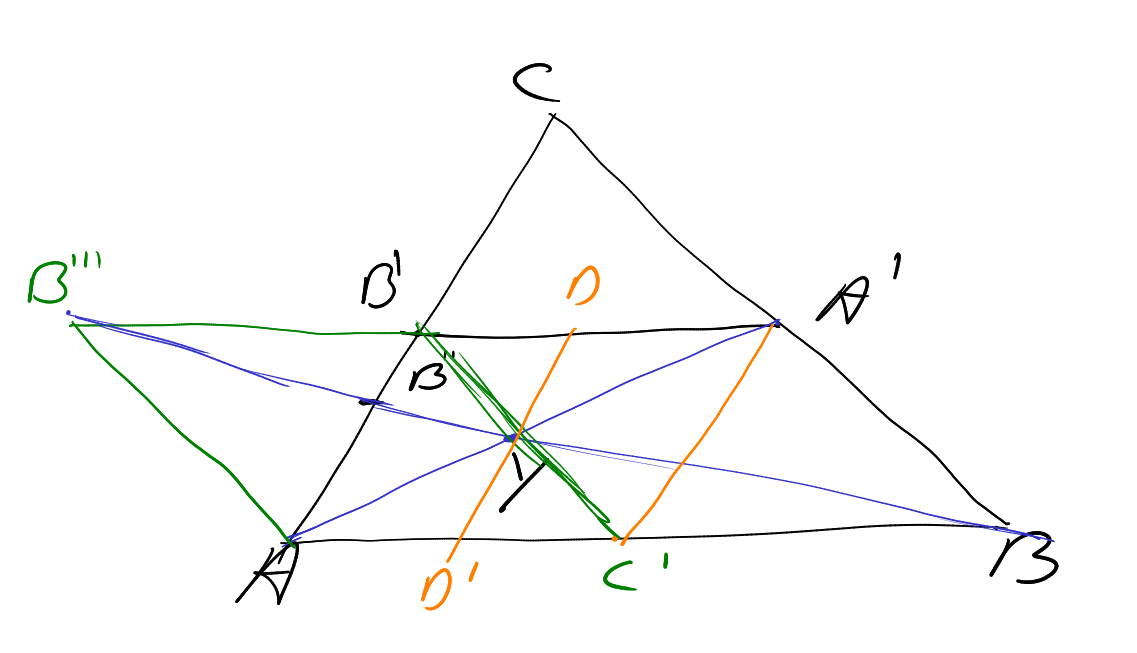
Ik heb $B'$ op zijn plaats gelaten en zijn opgeschoven versie $B''$ genoemd.
Verder is $C'$ het midden van $AB$, $D$ het midden van $A'B'$ en $D'$ het midden van $AC'$.
Verder heb ik $A'B'$ doorgetrokken tot $A'B'''$, zo dat $A'B'''=2A'B'$; dan is $ABA'B'''$ een parallellogram, net als $C'BA'B'$, $AC'B'B'''$ en $AC'A'B'$.
Verder zijn $B'A$, $DD'$ en $A'C'$ evenwijdig.
Om te bewijzen dat $Y$ op de lijn $BB'$ en dus op de diagonaal $BB'''$ ligt kijken we naar het snijpunt van de diagonalen $AA'$ en $BB'''$, we willen dat dat $Y$ is maar we noemen het even $Z$.
We weten dat $DZ$ en $B'B''$ evenwijdig zijn, dus $\angle B''B'B'''$ en $\angle ZDB'''$ zijn gelijk. verder geldt: $B'''D:B'''B'= 3:2$ ($B'D$ is de helft van $B'B'''$), en ook $DY:B'B''=3:2$ ($DZ=\frac12DD'=\frac12B'A$ en $B'B''=\frac13B'A$).
De driehoeken $B'''B'B''$ en $B'''DD'$ zijn dus gelijkvorming en $B''$ ligt dus op de diagonaal $BB'''$.
Dus $Z$ is het snijpunt van $AA'$ en $B''B$ en dat was nu onze $Y$.
kphart
|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 25 juli 2021
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|








 Dit is een reactie op vraag 92494
Dit is een reactie op vraag 92494 
