|
|
|
\require{AMSmath}



Re: Wiskunde olympiade
Bij de tweede vraag: wat moet ik doen met de sommatieteken? Als de n=oneindig, hoe kan je dan het juiste antwoord bereken?
k
Student universiteit BelgiŽ - maandag 16 maart 2020
Antwoord
Ik heb er maar 's een boomdiagram bij getekend. Dat doet wonderen!
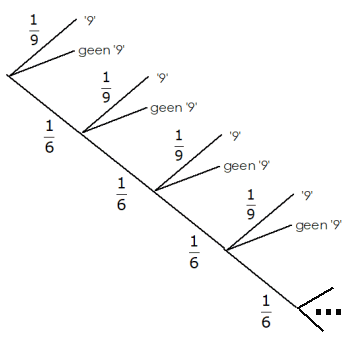
Als je niet dubbel gooit stopt ze met gooien. In dat geval heb je of '9' gegooid of je hebt 'geen 9' gegooid. Je moet maar 's kijken hoe je dat terug kunt vinden in het boomdiagram.
$
\eqalign{S = \frac{1}{9} + \frac{1}{6} \cdot \frac{1}{9} + \frac{1}{6} \cdot \frac{1}{6} \cdot \frac{1}{9} + \frac{1}{6} \cdot \frac{1}{6} \cdot \frac{1}{6} \cdot \frac{1}{9} + ...}
$
$
\eqalign{\sum\limits_{n = 0}^\infty {\frac{1}
{9}} \cdot \left( {\frac{1}
{6}} \right)^n}
$
De optelsom van alle kansen om 9 te gooien is de som van een meetkundige rij. Voor sommeerbare meetkundige rijen bestaat een mooie formule.

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 16 maart 2020
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|








 Dit is een reactie op vraag 89349
Dit is een reactie op vraag 89349 

