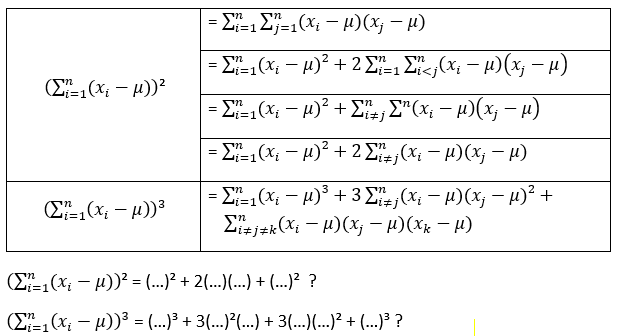|
|
|
\require{AMSmath}



Re: Re: Re: Variantie van steekproefgemiddelde
1000 x sorry, maar ik stel vast dat ik het nog niet helemaal door heb. In de nieuwe bijlage heb ik verschillende manieren geprobeerd die allemaal kloppen.
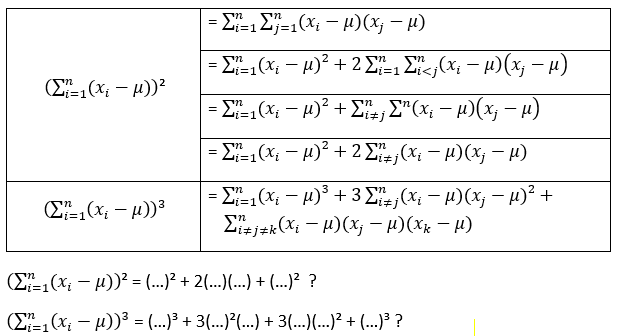
Nochthans is er nergens deze vorm met 3 termen te bespeuren: (a+b)2 = a2+2ab +b2. Wat is dan a en b? De sommatie kan i termen bevatten dus je kan niet a=(x1-u) en b=(x-u) doen. Idem bij (a+b)3.
M.a.w wat moet tussen de haakjes bij (…)2 + 2(…)(…) + (…)2 en bij (…)3 + 3(…)2(…) + 3(…)(…)2 + (…)3 ?
Valeri
Student universiteit België - woensdag 6 november 2019
Antwoord
Bij $(a+b)^2$ gaat het om het geval $n=2$, dus $a=x_1-\mu$ en $b=x_2-\mu$. Het geval $n=3$ kun je afkorten met $(a+b+c)^2$, dus $a=x_1-\mu$, $b=x_2-\mu$ en $c=x_3-\mu$.
Hoe groter de $n$ hoe meer termen; mijn suggesties waren er alleen om je een idee te geven van de gedaante van de som als je kleine aantallen termen neemt.
Als je $\bigl(\sum_{i=1}^n(x_i-\mu)\bigr)^2$ uitwerkt krijg je alleen die drie termen als $n=2$. In het algemeen krijgt je $n$ kwadraten en $n(n-1)$ gemengde termen; die komen in paren dus die $n(n-1)$ geven $2(\ldots)$ met tussen de haakjes dus $\frac12n(n-1)$ gemengde termen van de vorm $(x_i-\mu)(x_j-\mu)$ met $i < j$.
Als de derde macht neemt krijg je $n$ derde machten, $3n(n-1)$ termen van de vorm $(x_i-\mu)^2(x_j-\mu)$ met $i\neq j$ en $6\times\binom{n}{3}$ termen van de vorm $(x_i-\mu)(x_j-\mu)(x_k-\mu)$ met $i$, $j$ en $k$ verschillend.
kphart
|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 6 november 2019
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|








 Dit is een reactie op vraag 88668
Dit is een reactie op vraag 88668