WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Ongelijkheid oplossen

Beste

Ik ben vergeten hoe ik vergelijkingen moet oplossen. Ik zoek ook dat het dit keer staat dat een vergelijking niet gelijk is aan 0 bijvoorbeeld, maar kleiner dan 0. Maak dat iets uit bij het oplossen van vergelijkingen? Nogmaals erg bedankt voor de hulp.

Voorbeeld

$
\eqalign{\frac{{x^2 + 4x + 3}}
{{x^2 - x}} \leq 0}
$

Ik ben draad echt helemaal kwijt.
jan
Leerling bovenbouw havo-vwo - zaterdag 16 juni 2018

Antwoord

Om de ongelijkheid $
\eqalign{\frac{{x^2 + 4x + 3}}
{{x^2 - x}} \leq 0}
$ op te lossen maak je een tekenverloop van teller, noemer en breuk. De vraag is wanneer is de teller en/of de noemer gelijk aan nul, kleiner dan nul of groter dan nul...

De teller gelijk aan nul stellen geeft:

$
\eqalign{
& x^2 + 4x + 3 = 0 \cr
& (x + 3)(x + 1) = 0 \cr
& x = - 3 \vee x = - 1 \cr}
$

De noemer gelijk aan nul stellen geeft:

$
\eqalign{
& x^2 - x = 0 \cr
& x(x - 1) = 0 \cr
& x = 0 \vee x = 1 \cr}
$

Dat geeft voor de breuk 5 mogelijke gebieden met een breuk kleiner, groter of gelijk aan nul. Je moet wel uitkijken als de noemer nul is.

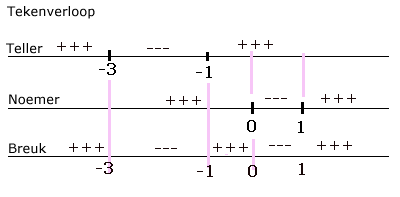
De oplossing is dan:

$
- 3 \leq x \leq - 1 \vee 0 < x < 1
$

Lukt dat?

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 16 juni 2018