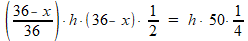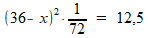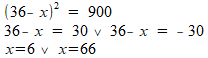|
|
|
\require{AMSmath}



Re: Re: Hoogtelijn driehoek
Beste
Bedankt voor uw antwoord. Helaas lukt het mij nog steeds niet.
Ik kom de volgende vergelijking uit:
(QP.PC)/2 = (AD.DC)/4
Vervolgens vul ik de waarde van de vergelijking in.
((((36-x)/36).h).(36-x))/2 = 36h/4
Maar hier blijf je toch met die onbekende h zitten?
Ruud
Ruud
Student Hoger Onderwijs BelgiŽ - zaterdag 17 juni 2017
Antwoord
Hallo Ruud,
Voor de overzichtelijkheid geef ik hier nog eens de betreffende figuur weer:
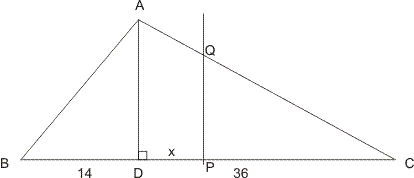
Jouw vergelijking is onjuist. De lijn QP moet de oppervlakte van de complete driehoek ABC in twee gelijke delen verdelen, niet alleen het rechter deel ADC. De vergelijking wordt dan:
(QP∑PC)/2 = (AD∑BC)/4
Ingevuld levert dit:
((((36-x)/36).h).(36-x))/2 = 50h/4
Hiermee is het probleem van de onbekende h niet opgelost, maar deze h valt uit je vergelijking. Iets overzichtelijker genoteerd is:
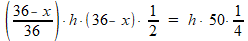
Je kunt links en rechts van het is-gelijk-teken delen door h, je krijgt:
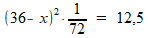
Verder uitwerken levert:
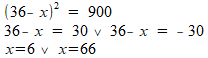
Uiteraard is alleen de oplossing x=6 relevant.
OK zo?

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 17 juni 2017
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2025 WisFaq - versie 3
|








 Dit is een reactie op vraag 84632
Dit is een reactie op vraag 84632