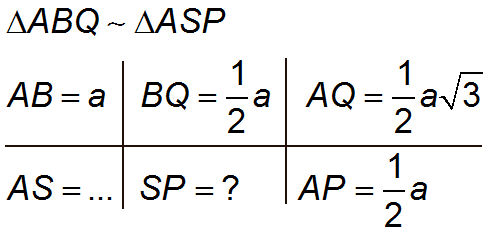|
|
|
\require{AMSmath}



Re: De oppervlakte en inhoud van een tetraŽder
Hallo,
Ik had een vraag over het gedeelte van uw uitleg:
Nu nog PS berekenen. Met behulp van het gegeven dat ABQ gelijkvormig is met ASP (ga na!) kan je PS berekenen.
PS=1/6∑a∑√3
Ik kom niet op de 1/6.
Is dit 1/2∑1/3=1/6.?
Mar dit doe je toch al in de vervolgstap?
Wanneer ik een verhoudingstabel maak, krijg ik:
AP∑BQ/AQ=PS
1/2a∑1/2a gedeelt door 1/2a√3=1/2a√3
Hoe bereken ik de 1/6?
Bij voorbaat mijn dank.
Groet Kees
Kees
Leerling bovenbouw havo-vwo - zaterdag 14 januari 2017
Antwoord
Volgens mij krijg je inderdaad:
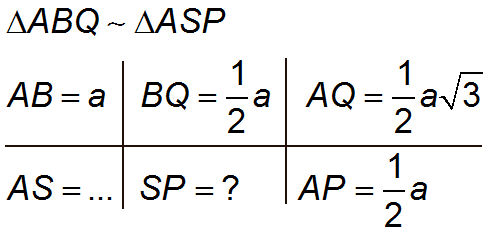
Maar dan:
$
\eqalign{
& SP \cdot \frac{1}
{2}a\sqrt 3 = \frac{1}
{2}a \cdot \frac{1}
{2}a \cr
& SP = \frac{{\frac{1}
{4}a^2 }}
{{\frac{1}
{2}a\sqrt 3 }} = \frac{{a^2 }}
{{2a\sqrt 3 }} = \frac{a}
{{2\sqrt 3 }} \cr
& SP = \frac{a}
{{2\sqrt 3 }} \cdot \frac{{\sqrt 3 }}
{{\sqrt 3 }} = \frac{{a\sqrt 3 }}
{{2 \cdot 3}} = \frac{{a\sqrt 3 }}
{6} = \frac{1}
{6}a\sqrt 3 \cr}
$
...en dat is het dan!

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 14 januari 2017
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2025 WisFaq - versie 3
|








 Dit is een reactie op vraag 7910
Dit is een reactie op vraag 7910