|
|
|
\require{AMSmath}



Driehoek van Pascal inkleuren
Ik heb iets gelezen over structuren in de driehoek van Pascal. Als je bijvoorbeeld de getallen die deelbaar zijn door 9 kleurt, krijg je een bepaalde structuur te zien. Deze structuren zijn per getal erg verschillend. Bij het getal 11 krijg je allemaal driehoeken van gelijke grootte, maar 1 driehoek is veel groter (helemaal onderin). Bij het getal 4 lijkt de structuur onregelmatig. Hoe komt het dat die structuren zo verschillend zijn en welke functie hebben die structuren voor mij?
Anneke
Leerling bovenbouw havo-vwo - dinsdag 25 februari 2003
Antwoord
Je weet vast wel hoe je de driehoek van Pascal maakt. Aan de zijden staan 1-en en in het midden is elk getal de som van de twee getallen die direct boven tegenaan liggen.
Zoals hieronder bijvoorbeeld:
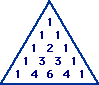
Dit kun je net zo ver door laten gaan als je maar wilt.
Als je om de getallen een vierkantje zet en dan de vierkantjes inkleurt, krijg je hele regelmatige patronen.
Eerst maar eens een voorbeeld voor delen door 2. In de volgende tekening zijn de getallen die rest 1 geven bij deling door 2 (oneven getallen) rood gekleurd. De even getallen hebben geen kleur.

Je ziet dat de patronen steeds terugkeren. Hoe komt dit nu.
Elk getal is ontstaan door de twee getallen erboven op te tellen.
Algemeen kunnen we zeggen dat als we twee even getallen optellen we weer een even getal krijgen. Als we twee oneven getallen optellen krijgen we ook altijd weer een even getal en als we een oneven en een even getal optellen is de som oneven. Probeer dat maar eens te bewijzen. Vertaald naar onze driehoek betekent dat dat het vakje met daar direct boven een wit en een rood vakje weer rood gekleurd moet worden (oneven + even = oneven). Hebben twee vakjes naast elkaar dezelfde kleur dan is het vakje erondertussen wit (even+even=even en oneven+oneven=even).
Dit is ook de reden dat de figuren steeds terug keren.
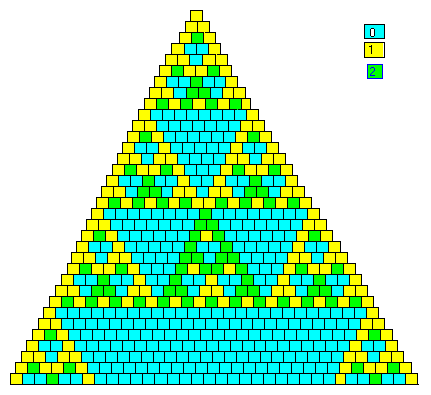
Hetzelfde kun je doen voor de resten bij het delen door andere getallen. Neem bijvoorbeeld 3. Dan kun je de getallen die bij deling door 3 rest 1 geven geel kleuren en de getallen die bij deling door 3 rest 2 geven groen, de drievouden worden blauw. Dan staat dus onder een groen en geel vakje een blauw vakje (zie hieronder)
Je kunt natuurlijk ook alleen de getallen met rest 1 een kleurtje geven.
Als je deelt door grotere getallen zijn er meer mogelijk resten en zul je ook weer andere patronen krijgen.
Tja, en wat de functie hiervan is.........

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 26 februari 2003
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2025 WisFaq - versie 3
|












