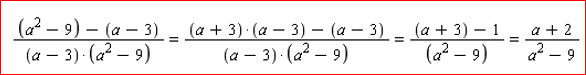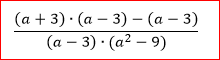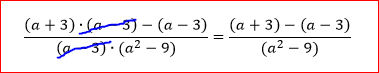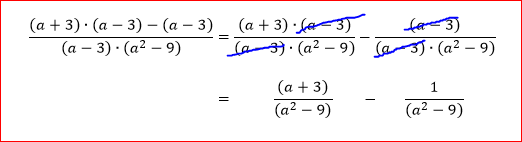|
|
|
\require{AMSmath}



Re: Breng onder één noemer en vereenvoudig
Dag Thijs,
Bedankt voor de uitleg. Ik worstel ook met de opgave.
Wat ik niet snap is waarom 2x (a-3) uit de teller verdwijnt, en dus -1 wordt, terwijl je maar 1x kunt wegstrepen tegen de noemer.
Ik loop vast op
(a+3) - (a-3)
____________
(a2-9)
Hoe kom je dan op:
(a+3) - 1
____________
(a2-9)
???
Zou je dit kunnen / willen verduidelijken?
Alvast bedankt.
Mvg Iris
Iris
Ouder - woensdag 26 augustus 2015
Antwoord
Dag Iris,
Dat is een tijd geleden dat ik nog vragen heb beantwoord via Wisfaq, ik geloof de laatste van augustus 2012. Maar ik zal hier wel nog op ingaan.
Na even teruggezocht te hebben, was mijn laatste vergelijking in mijn vorige antwoord als volgt:
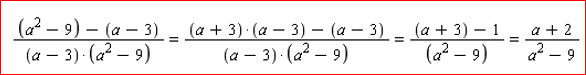
Hierin staat nergens het uitgangspunt waar jij nu van uit gaat, zijnde:
(a+3) - (a-3)
-------------
(a2-9)
Van deze deling naar je gevraagde resultaat, kan inderdaad ook niet. Dus daar kan ik je dan ook niet mee helpen ;) En gelukkig heb ik dat ook niet zo gesteld toentertijd.
Maar ik zie wel je denkfout, denk ik. Ik ga er even vanuit dat je het nog volgt t/m de volgende breuk:
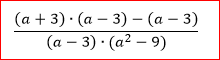
Jij denkt dat je maar 1 keer de (a-3) weg mag strepen (of 'wegdelen' zoals het correct heet):
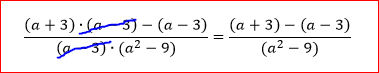
Maar bovenstaande, is een foute gedachte. Het regeltje zegt iets van:
"In een breuk (of deling) mogen in de teller en in de noemer, gelijke factoren weg gedeeld worden" - ... met enkele uitzonderingen daargelaten...
Maar als we goed kijken naar deze breuk, zien we dat de teller van deze breuk, uit twee delen bestaat (twee 'termen' heten dat). Er staat namelijk een - tussen. Dan concludeer je eigenlijk dat die breuk, het resultaat is van twee gelijknamige breuken (met gelijke noemers) die van elkaar afgetrokken zijn. Want een regel zegt ook:
"Twee gelijknamige breuken (gelijke noemers) kun je bij elkaar optellen of aftrekken, door eenvoudig de beide tellers bij elkaar op te tellen of van elkaar af te trekken, en daar die betreffende noemer onder te zetten."
Dus ik ga die breuk opsplitsen in twee losse breuken, van elkaar afgeteld. Dan heb je dus 2 breuken, waarbij je dat 'trucje' van wegdelen kunt doen:
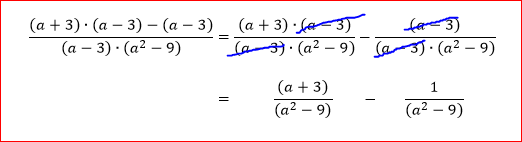
Als je van die 2 breuken vervolgens weer 1 breuk maakt (tellers van elkaar aftrekken en 1 noemer schrijven), dan heb je het gezochte resultaat.
Hopelijk had je er wat aan.
Met vriendelijke groet,
Thijs Bouten

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 27 augustus 2015
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2025 WisFaq - versie 3
|








 Dit is een reactie op vraag 65428
Dit is een reactie op vraag 65428