|
|
|
\require{AMSmath}



Re: Re: Wiskunde Olympiade opgave 1994-A3
Oké erg bedankt, dit is mijn laatste vraag.
Weet u misschien waar er een uitwerking van deze opgave te vinden is? Ik loop namelijk op een bepaald punt vast.
groetjes,
oscar
Oscar
Leerling bovenbouw havo-vwo - zaterdag 4 juli 2015
Antwoord
Hallo Oscar,
Ik weet niet waar je een uitwerking kunt vinden. Je kunt natuurlijk wel altijd bij ons hulp vragen.
Ik weet niet waar je vastloopt. Heb je dit al geprobeerd (zie onderstaande figuur):
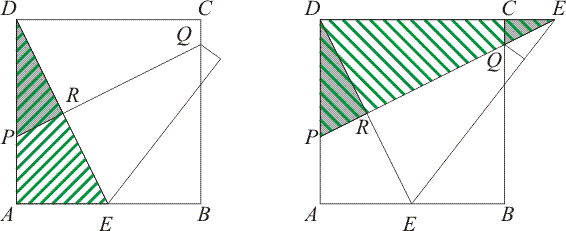
Je weet al dat DE en PQ elkaar loodrecht snijden. Dat betekent dat de driehoeken DRP en DAE gelijkvormig zijn, zie linker figuur. In driehoek DAE ken je alle zijden (Pythagoras), dus in driehoek DRP zijn ook alle zijden te berekenen.
In de rechter figuur zijn nog eens drie gelijkvormige driehoeken aangegeven, waaronder DRP waarvan je alle zijden kent. Van al deze driehoeken zijn dus alle zijden te berekenen.
Hiermee zou met een beetje puzzelen (optellen en aftrekken) de lengte van PQ te berekenen moeten zijn. Lukt dit nu?
PS: Na een tip zie ik dat je PQ sneller kunt berekenen, zie onderstaande figuur:
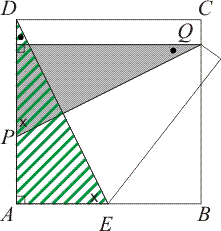
De grijze en gestreepte driehoeken zijn congruent (HZH). Dan geldt dus: PQ=ED. Met Pythagoras had je ED al berekend, denk ik.

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 4 juli 2015
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2025 WisFaq - versie 3
|








 Dit is een reactie op vraag 75981
Dit is een reactie op vraag 75981 


