|
|
|
\require{AMSmath}



Re: Vector vergelijking
Ik wil je bedanken voor de sublieme uitleg van de opgave.
Ik heb noch een opgave waar ik niet uit kom
als volgt:
De resultante uit de vorige uitgave nl F(res)30,49 met
alpha 6,1 gr, moet nu twee krachten C(140 gr.)en 27(y gr)
compenseren.
gevraagd worden kracht C(140 gr) en de hoek van 27( y gr)
bij voorbaat dank voor de hulp
joep
Ouder - donderdag 2 juli 2015
Antwoord
Hallo Joep,
Als ik het goed begrijp, zoek je twee krachten die opgeteld de kracht Fres in onderstaande figuur opleveren. Eén kracht heeft een werklijn met richting 140° t.o.v. de positieve x-as, de tweede kracht heeft als grootte 27.
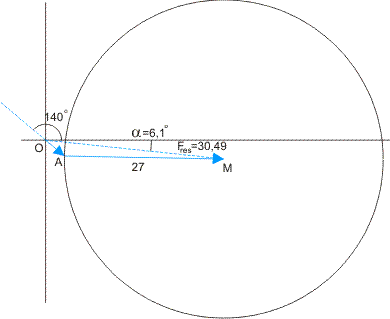
Je vindt deze krachten met behulp van de 'kop-staart-methode': wanneer je een aantal (kracht)vectoren optelt, kan je de 'staart' van de tweede vector op de 'kop' van de eerste vector plaatsen. Op de kop van de tweede vector zet je weer de staart van de volgende vector, enz. De resultante (kracht)vector loopt dan van de staart van de eerste vector naar de kop van de laatste vector.
In dit geval: de kop van de tweede vector (van grootte 27) moet uitkomen op de kop van de resultante. Teken dus een cirkel met middelpunt de kop van Fres en straal 27. De staart van de gezochte vector ligt ergens op deze cirkel.
Teken ook de werklijn van de eerste kracht C (140° t.o.v. de positieve x-as). De staart van deze vector ligt in de oorsprong, de kop moet ergens op de cirkel liggen. Zo vind je punt A: de kop van de eerste kracht C, tevens de staart van de vector met grootte 27. Je ziet dat de eerste vector in negatieve richting loopt, wanneer we de genoemde 140° positief noemen.
Nu nog de berekening van de grootte van kracht OA, en de richting van kracht AM:
In de figuur zie je: hoek MOA = 180-(140+6,1)=33,9 °. Nu is OA te berekenen met behulp van de cosinusregel. Er geldt:
AM2 = OA2+OM2 - 2·OA·OM·cos(hoek MOA)
Hierin is OA de enige onbekende.
Met behulp van de sinusregel is hoek AMO te berekenen:
OA/sin(AMO) = AM/sin(MOA)
Hierin is hoek AMO de enige onbekende. De richting van AM t.o.v. de positieve x-as is gelijk aan deze hoek, verminderd met 6,1° (richting van Fres onder de positieve x-as).

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 3 juli 2015
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2025 WisFaq - versie 3
|








 Dit is een reactie op vraag 75956
Dit is een reactie op vraag 75956 

