|
|
|
\require{AMSmath}



Bezierkromme
Ik heb een kwadratische bezierkromme met de volgende punten: P0=(0,0) en P2=(1,0). Ook is de top van de kromme gegeven (deze kan variŰren maar we nemen (0.25,0.75) als voorbeeld). Ik wil een formule opstellen om de positie van P1 te kunnen berekenen, is dit mogelijk?
Alvast bedankt
Jarvis
Student hbo - maandag 13 april 2015
Antwoord
Volgens Wikipedia | Kwadratische Bezierkromme moet gelden:
$
B(t) = \left( {1 - t} \right)^2 P_0 + 2t\left( {1 - t} \right)P_1 + t^2 \cdot P_2 \,\,voor\,\,t \in [0,1]
$
Met P0=(0,0), P1=(x,y) en P2=(1,0) geldt:
$
\begin{array}{l}
B(t) = \left\{ \begin{array}{l}
2t\left( {1 - t} \right)P_1 + t^2 \\
2t\left( {1 - t} \right)P_1 \\
\end{array} \right. \\
B(t) = \left\{ \begin{array}{l}
2t\left( {1 - t} \right) \cdot x + t^2 \\
2t\left( {1 - t} \right) \cdot y \\
\end{array} \right. \\
\end{array}
$
Oftewel:
$
\left\{ \begin{array}{l}
x = \frac{{4t^2 - 1}}{{8t(t - 1)}} \\
y = \frac{3}{{8t(1 - t)}} \\
\end{array} \right.
$
Voor de 'top' van de kromme geldt:
$
y' = 0 \Rightarrow t = \frac{1}{2}
$
Invullen geeft:
$
\begin{array}{l}
\left\{ \begin{array}{l}
x = \frac{{4\left( {\frac{1}{2}} \right)^2 - 1}}{{8 \cdot \frac{1}{2}(\frac{1}{2} - 1)}} = 0 \\
y = \frac{3}{{8 \cdot \frac{1}{2}(1 - \frac{1}{2})}} = 1\frac{1}{2} \\
\end{array} \right. \\
B(t) = \left\{ \begin{array}{l}
t^2 \\
2t\left( {1 - t} \right) \cdot 1\frac{1}{2} \\
\end{array} \right. \\
B(t) = \left\{ \begin{array}{l}
t^2 \\
3t\left( {1 - t} \right) \\
\end{array} \right. \\
\end{array}
$
...en dan ben je er wel. Het punt $P_1$ heeft als co÷rdinaten $(0,1\frac{1}{2})$.
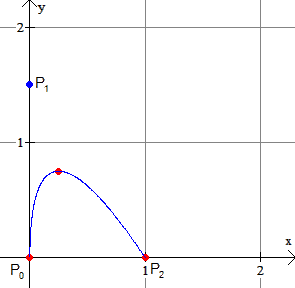
Zoiets moet het zijn. Zou het daarmee lukken?

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 13 april 2015
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2025 WisFaq - versie 3
|










