|
|
|
\require{AMSmath}



Labyrint
Bij onderzoek naar intelligentie van ratten wordt soms gebruik gemaakt van een gangenstelsel: een zogenaamd T-labyrint. Hieronder zie je zo’n T-labyrint.
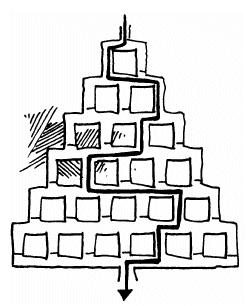
In elk van de verticaal getekende gangen zit een klap- deurtje, dat slechts in één richting kan worden gepasseerd. Dat verhindert dat een rat terug naar boven kan lopen. Een rat kan langs een groot aantal routes van de ingang naar de uitgang lopen. Hierboven is zo’n route getekend.- De totaal aantal routes is 5040. Dat heb ik als volgt berekend: 2x3x4x5x6x7 want bij de eerste deurtjes heb je 2 gangetjes daarna 3 etc.
- Hoeveel kortste routes zijn er van de ingang naar de uitgang?
Nu begrijp ik niet hoe ik vraag b. moet oplossen, zou u me kunnen helpen?
Alvast bedankt!
Laura
Leerling bovenbouw havo-vwo - zondag 14 december 2014
Antwoord
Vraag a. lijkt me helemaal goed. Vraag b. is iets lastiger. Als je kijkt naar waar de rat kan gaan zonder om te lopen dan krijg je het volgende roosterdiagram:
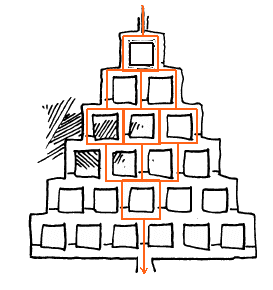 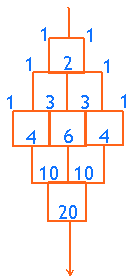
Dat komt me bekend voor. Dat is een stuk van de driehoek van Pascal. Kennelijk zijn er 20 verschillende kortste routes:
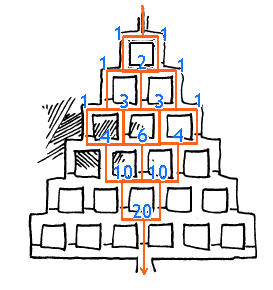
Helpt dat?

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 14 december 2014
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2025 WisFaq - versie 3
|













