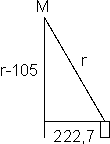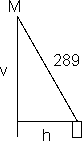|
|
|
\require{AMSmath}



Bepaling dieptes van een bolsegment in een vierkant raster
Hoi wisfaq, ben bezig met een houten kunstwerk. Heb een raster van 8x8 vierkante houten staafjes. Elk staafje is 45 x 45 mm doorsnede, max hoogte 105 mm. Totale afmeting raster is dus 358 x 358 x 105 mm (het blijft hout :-)).
Ik wil de 64 staafjes zodanig op lengte afkorten dat het lijkt alsof er een bolsegment is uitgehaald, max diepte van die bol in het midden is dus 105 mm. Alles haaks afkorten ook.
Met meten (=weten :-))lukt het me wel om een cirkelsegment uit de middelste rij te bepalen (max 105 mm diep), maar dan zijn alle hoeken even hoog en dat is niet mooi qua diepte beleving. Het mooiste is nl als alleen de 4 uiterste staafjes 105 mm zijn, dus moet van de diagonale lijn van het raster uitgaan voor bepaling straal bolsegment. Maar dan loop ik hopeloos vast, kunnen jullie me helpen?
- Ik kan wel een cirkelsegment tekenen met de diagonaal van het raster als uitgangspunt (vierkant zijdes 358 mm dus diagonaal = 506 mm - Pythagoras ken ik nog wel :-)), zodanig dat dan de max diepte 105 mm is. Tekenen en meten dus. Potlood aan een touwtje+duimstok-werk.
- Dan zou ik wel de lengte van de staafjes kunnen meten die langs de diagonalen lopen van het raster.
- Maar dan heb ik geen idee hoe je dan overgaat tot bepaling lengte staafjes langs de middellijnen.
Snappen jullie mijn vraag? Heb mn best gedaan om het zo exact mogelijk te verwoorden.

Een cad-cam tekenaar schudt dit misschien in een minuut uit zijn computer, maar dat ben ik niet. Dus dacht ik aan jullie wiskundigen. Het is denk ik juist een leuk vraagstuk voor jullie want zo moeilijk kan het nou ook weer niet zijn. Maar leg het maar eens uit zodat deze jongen met VWO wiskunde A&B dertig jaar geleden heeft gehad het ietsiepietsie kan volgen...
Groet en graag tot horens / mailens, keep up the good work
Wouter 
Wouter
Iets anders - woensdag 10 september 2014
Antwoord
Beste Wouter,
Als ik je vraag goed begrijp, wil je de hoogte van de blokjes zodanig maken dat de bovenkant van de blokjes op een denkbeeldige bol liggen, alsof deze de onderkant van een skippy-bal raken. De bol moet zo groot zijn dat de blokjes op de vier hoekpunten 105 mm hoger zijn dan de vier middelste blokjes.
Wanneer dit inderdaad de opgave is, dan is het mooi dat je Pythagoras nog beheerst, want meer hebben we niet nodig. Ik zal laten zien hoe je berekent hoe je de middens van elk blokje op de bol krijgt. Dit rekent het gemakkelijkst, en ziet er denk ik ook het mooist uit.
Eerst berekenen we de straal r van de denkbeeldige skippy-bal. Denk je in dat we een touwtje vastmaken in het middelpunt van deze bal. De lengte van het touwtje is gelijk aan de straal van de bal. Wanneer het touwtje recht naar beneden hangt, komt het tot het diepste punt van je kunstwerk. Wanneer we het touwtje opzij trekken, tot boven het midden van een blokje op een hoekpunt, dan moet het uiteinde van het touwtje 105 mm omhoog gegaan zijn.
In x-richting trekken we het touwtje 3,5 x 45 mm opzij (let op: tot het midden van het 4e blokje), dit is 157,5 mm. In y-richting is de verplaatsing ook 157,5 mm. Met Pythagoras berekenen we dat we het touwtje in diagonale richting 222,7 mm opzij hebben getrokken. Zover was je al, begrijp ik.
We eisen nu dat de verticale afstand tussen middelpunt bol en uiteinde touwtje 105 mm korter is geworden, deze bedraagt nu dus (r-105) mm. Deze afstanden vormen samen met het touwtje een rechthoekige driehoek, zie figuur.
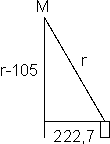
Dankzij Pythagoras weten we:
(r-105)2 + 222,72 = r2
Oplossen van de vergelijking levert:
r=289 mm.
Conclusie: de skippybal heeft een straal van 289 mm, het middelpunt M ligt dan ook 289 mm boven het midden van het raster.
Voor het berekenen van de hoogte van andere blokjes gebruiken we dezelfde truc, maar nu met bekende r en onbekende hoogte van een blokje. Als voorbeeld neem ik, vanuit het midden gerekend, het 2e blokje in x-richting en het 3e blokje in y-richting:
Het midden van dit blokje ligt op:
x = 1,5·45 = 67,5 mm
y = 2,5·45 = 112,5 mm
De horizontale afstand vanuit het middelpunt noem ik h. Dan geldt:
h2 = 67,52 + 112,52 = 17212,5
Volgens Pythagoras in verticaal vlak geldt (zie figuur):
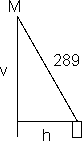
h2 + v2 = r2
v2 = r2 - h2
v2 = 2892 - 177212,5 = 66308,5
v = √66308,5 = 257,5
De hoogte van dit blokje wordt:
hoogte = r - 257,5
hoogte = 289 - 257,5
hoogte = 31,5 mm.
Lukt het nu om op dezelfde wijze de hoogte van de overige blokjes te berekenen?
PS.: omdat je een even aantal blokjes naast elkaar hebt, raken de middelste vier blokjes op dezelfde wijze aan het middelpunt van het raster en worden deze dus allevier even hoog. Misschien vind je dit niet zo mooi. Wellicht valt te overwegen om een oneven aantal blokjes naast elkaar te nemen (7×7 of 9×9 bv). Dan valt het midden van het raster samen met het midden van een enkel blokje, en vind je nooit twee even hoge blokjes naast elkaar.

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 11 september 2014
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2025 WisFaq - versie 3
|