|
|
|
\require{AMSmath}



Re: Re: Berekenen lengte boog
Heel erg bedankt voor het doorsturen van de berekeningen. De berekeningen zijn volledig duidelijk, maar er blijft voor mij een probleem. Ik begrijp niet vanwaar de waarde 70 komt. 70 is het verschil tussen het hoogste en het laagste punt en kan toch niet op deze manier gebruikt worden. Waar ben ik fout.
Annie
Iets anders - dinsdag 22 april 2014
Antwoord
Hallo Annie,
In een aanvullende mail heb je duidelijk gemaakt dat ik de situatie niet goed had begrepen. Onderstaande figuur geeft de situatie beter weer:
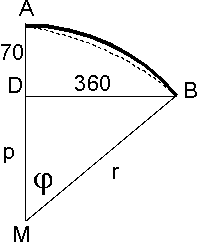
Punt A is het hoogste punt van de boog, dit ligt 70 cm boven punt B.
Het is mij niet helemaal duidelijk of de boog bij A horizontaal begint (de dikke lijn) of dat de boog bij A al schuin naar beneden loopt (gestippelde lijn). Voor de lengte van de gestippelde lijn hebben we meer gegevens nodig, bijvoorbeeld de helling van de boog bij A.
De booglengte van de dikke lijn kunnen we wel berekenen, op ongeveer dezelfde manier als in mijn vorige antwoord:
In de figuur zien we:
MA = MB = r
p = r-70, dus r = p+70
Volgens Pythagoras geldt in driehoek MDB:
r2 = p2+3602
(p+70)2 = p2+3602
p2+140p+4900 = p2+129600
140p = 129600-4900 = 124700
p = 124700/140 = 890,7
r = p+70 = 960,7
In dezelfde driehoek zien we:
tan(j) = 360/p = 0,404
j = atan(0,404) = 0,384 rad.
Booglengte AB = j×r = 0,384x960,7 = 369,0 cm
Is hiermee je vraag wel beantwoord?

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 25 april 2014
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2025 WisFaq - versie 3
|








 Dit is een reactie op vraag 72747
Dit is een reactie op vraag 72747 

