WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Vraagstuk met vierkantswortel

Hallo,

Kan u mij helpen met volgende vraag?

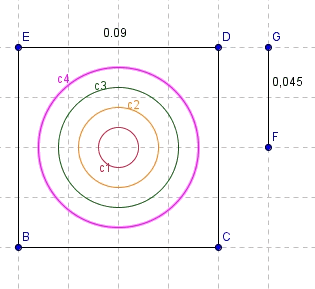
'In een schietstand wordt er een doel op 100 meter geplaatst. Het heeft de vorm van een vierkant en is 0,81m² groot. Afstand tussen de rand van het vierkant en de buitenste cirkel is gelijk aan de afstand tussen al de cirkels onderling en de straal van de roos. Hoe verhoudt de oppervlakte van de roos zich tegenover van de totale oppervlakte van de buitenste cirkel?'

$\rightarrow$We weten dus dat 1 zijde = 0,09 cm² maar verder zit ik vast..

Alvast bedankt,

Feline
feline
Overige TSO-BSO - maandag 14 oktober 2013

Antwoord

Hoi Feline,

Ik weet niet of ik je vraag goed begrijp, want de schietafstand doet er volgens mij niet zoveel toe. Ook neem ik aan dat je de kortste afstand van de vierkante zijde tot de cirkels bedoelt. Ook weet ik niet hoeveel cirkels er zijn dus een concreet getal kan ik je niet geven. Echter geef ik je ( hopelijk ) een idee voor de aanpak.

$
\begin{array}{l}
r_{c1} = \frac{{0,45}}{{n + 1}} \\
r_{c2} = 2.r_{c1} \\
r_{cn} = nr_{c1} \Rightarrow \frac{{\pi r_{c1}^2 }}{{\pi (nr_{c1} )^2 }} = \frac{1}{{n^2 }} \\
\end{array}
$

n = aantal cirkels

Is dit wat je bedoelde?

mvg DvL

DvL

Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 14 oktober 2013