WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Buigpunten berekenen

Hallo,

Ik moet een functieonderzoek van van volgende functie:
³Ö(x³-3x+2).
Ik heb gevonden dat er een knikpunt is in x = 0, maar zit altijd vast bij het berekenen van buigpunten vanuit de tweede afgeleide. Ik denk dat ik iets fout doe met het wegwerken van de wortel in de noemer.

Mijn tweede afgeleide heb ik gevonden denk ik:
y'' = 2x·³Ö((x³-3x+2)²) - ((2x⁴-4x²+2))
³Ö((x³-3x+2)²)
³Ö((x³-3x+2)⁴)

hieruit moet ik dan de nulpunten berekenen, zodat ik daarna kan zien of er buigpunten aanwezig zijn, volgens de oplossing is er een buigpunt in -2.

Alvast bedankt
Lien
Student universiteit België - woensdag 10 november 2010

Antwoord

Hallo

Het knikpunt heb je voor x=1!!

De eerste afgeleide is gelijk aan :

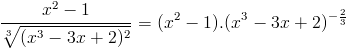
Om hiervan nogmaals de afgeleide te berekenen is het gemakkelijker deze vorm te schrijven als een product en dan de afgeleide van dit product te berekenen.
Dit wordt :

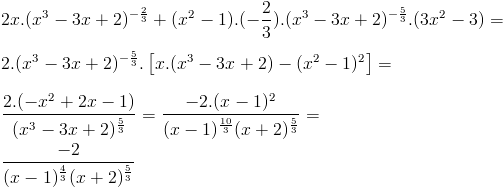
x=1 is dus een dubbel nulpunt en x=-2 is inderdaad een enkelvoudig (oneven) nulpunt, dus heb je hier een buigpunt.
De eerste afgeleide was hier onbepaald, dus de buigraaklijn loopt verticaal.

Ok?

Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 10 november 2010

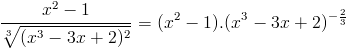
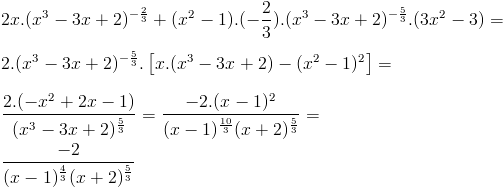
Re: Buigpunten berekenen