WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Driehoek met cosin en sin regel

Beste Wisfaq,

Ik ben het volgende tegen gekomen waar ik zelf maar niet uit kom. Ik loop richting het einde steeds vast.

Verhaaltje:
Flap uitslag van een vliegtuigje om de lift te berekenen daar moet je de koorde voor weten, de echte uitslag van de flap is dus niet zo belangrijk maar kan wel gebruikt worden om de echte koorde uitslag te berekenen.

Dit zijn mijn gegevens:
A = onbekend
B = (3/4) c
C = (1/4) c

Alpha = x [variabel]
Beta = Gevraagd
Gamma = onbekend

Ik zoek een formule in de form van:
Beta = functie van alpha

PS. B = (3/4) c - hier staat c voor een lengte van het besturingsvlak. (vanaf 25% beweegt het)
Vincen
Student hbo - zaterdag 16 januari 2010

Antwoord

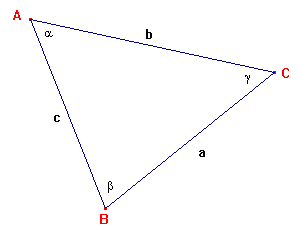
Gevraagd: bij gegeven b en c en $\alpha$ de grootte van $\beta$.

Bereken eerst a met de cosinusregel.

a²=b²+c²-2bc·cos$\alpha$

Vervolgens met de cosinusregel kan je dan $\beta$ berekenen.

b²=a²+c²-2ac·cos$\beta$

Als je één formule wilt kan dat natuurlijk ook. Je moet de formule dan nog even 'omschrijven' maar dat moet je dan nog maar 's proberen...

Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 19 januari 2010