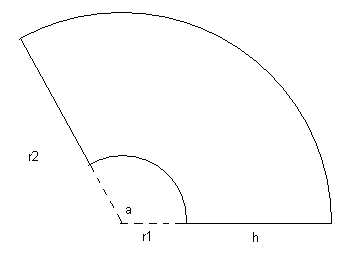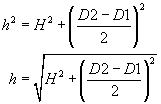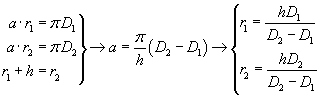|
|
|
\require{AMSmath}



De vorm van de uitslag van een conus berekenen
Hallo wiskundigen,
kunnen jullie mij helpen met het berekenen van de vorm van de uitslag van een afgeknotte conus? gegeven zijn de diameter van de bovenkant, de hoogte en de onderkant.
Ik heb dit nodig omdat ik regelmatig dergelijke vormen uit rubber moet snijden.
Alex
Iets anders - vrijdag 27 februari 2009
Antwoord
Ik ben niet zo handig met plaatjes als sommige van mijn collega's, maar toch maar een poging. De afgeknotte kegel waarvan je de uitslag zoekt, zie je hieronder.
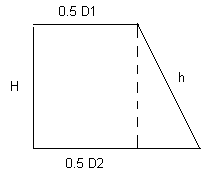
Hierbij is H de hoogte die je hebt, D1 de diameter aan de bovenkant, D2 de diameter aan de onderkant. h is de lengte van de schuine zijde van de afgeknotte kegel. Deze heb je nodig in de uitslag, die er namelijk zo uitziet:
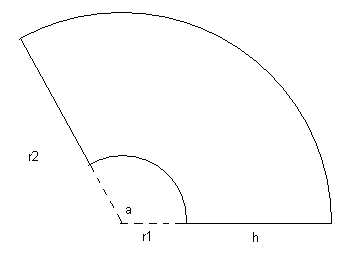
De waarde van h kan je uitrekenen door de stelling van Pythagoras toe te passen in het driehoekje aan de rechterkant van het bovenste plaatje:
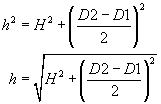
Dan heb je alleen nog de hoek a in het onderste plaatje, en de lengtes r1 en r2 te weten. Omdat de lengte van de delen van de cirkels in dit plaatje gelijk moeten zijn aan de omtrekken van de cirkels in je uiteindelijke conus, geldt:
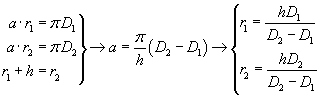
Zodat je alle waarden hebt voor de uitslag van de conus in het tweede plaatje. Succes!
Bernhard
|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 27 februari 2009
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2025 WisFaq - versie 3
|