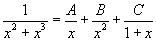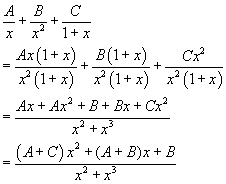|
|
|
\require{AMSmath}



Teller constante noemer 3de graad
de opgave is $\int{}$dx/(x3+x2)
ik ontbind de noemer als volgt x.x2.(x+1)
verder geraak ik niet omdat je toch links een functie moet hebben om dan alles gelijk te stellen en de noemer weg te laten en dan A,B,C uit te zoeken.
ik heb het zo eens geprobeerd $\int{}$1/x+$\int{}$1/x2+1/(x+1)
dan kom ik uiteindelijk ln(x)-1/x+ln(x+1)
kan dit kloppen of kunnen jullie mij wat wijzer maken.
misschien ik kan dan ook beginnen aan de volgende oefening beginnen waar ik ook niet aan uit kan omdat er weer een constante is in de teller $\int{}$dx/x4+x2
alvast hartelijk bedankt
oscar
3de graad ASO - zondag 20 januari 2008
Antwoord
Je begint inderdaad goed. Het is verstandig om hier breuksplitsen toe te passen. Dit werkt prima met jouw methode
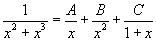
Jij kiest hier A,B en C gelijk aan 1. Dit is echter niet juist.
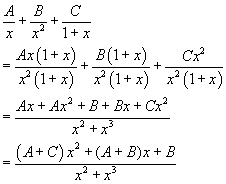
De teller hiervan moet nu gelijk zijn aan 1. (Waarom?)
Hieruit volgt
A+C=0
A+B=0
B=1
Het integreren zal dan niet moeilijk meer zijn. En denk om de integratieconstante!
Bernhard
|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 20 januari 2008
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2025 WisFaq - versie 3
|