|
|
|
\require{AMSmath}



Raaklijnen met e
Gegeven zijn de functies f(x) = ex-3 en g(x) = e2x+p (lineaire functie)- voor welke p heeft de vergelijking f(x)=g(x) geen oplossingen?
Door het punt (2,0) gaan twee raaklijnen aan de grafiek van f. Deze raaklijnen raken de grafiek van f in de punten P en Q.- bereken de afstand tussen P en Q in 2 decimalen nauwkeurig.
Groetjes
kim
Leerling bovenbouw havo-vwo - vrijdag 21 april 2006
Antwoord
a)
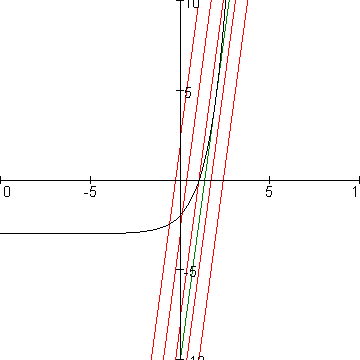
De richtingscoefficient van de rechte lijn is e^2.
Als je p zo kiest dat de rechte lijn de raaklijn is aan de grafiek van f in het punt met x=2 dan heeft deze lijn precies 1 punt gemeen met de grafiek van f.
In bovenstaand plaatje heb ik in groen de raaklijn aan de grafiek van f in (2,f(2)) getekend en in rood een aantal lijnen evenwijdig aan die raaklijn.
We stellen de vergelijking van de raaklijn in (2,f(2)) op:
y=e2(x-2)+e2-3
dus
y=e2x-2e2+e2-3
y=e2x-e2-3
Als we p kleiner kiezen dan -e2-3 heeft de grafiek van g(x) dus geen punten gemeen met de grafiek van f.
2)
Voor P en voor Q geldt dat de raaklijn in dit punt door het punt (2,0) moet gaan.
De raaklijn in een willekeurig punt (p,f(p)) heeft als vergelijking
y=ep(x-p)+ep-3
Invullen van x=2 en y=0 levert
ep(2-p)+ep-3=0.
De oplossingen van deze vergelijking zijn de x-coordinaten van P en Q.
Deze vergelijking kun je het beste oplossen met je GRM.
Vervolgens bereken je ook de y-coordinaten van P en van Q en de afstand.
groetjes

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 21 april 2006
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2025 WisFaq - versie 3
|










