|
|
|
\require{AMSmath}



Stelling van Thales
Hoe kan ik de stelling van Thales gebruiken voor deze vraag:
Je hebt een cirkel met middenpunt M. Verder ligt er in de cirkel een punt F. De vraag is vanuit welk punt R op de cirkel ik moet beginnen te lopen naar M zodat ik precies op de helft van mijn wandeling even ver van M als van F als van de cirkel af ben (punt D)? Ik loop recht naar M toe (dus op de straal).
Ik weet dat je de middelloodlijn op MF moet tekenen en dat op die lijn het punt D ligt waarop ik even ver van M als van F als van de cirkel ben. Ook weet ik dat de afstand van dat punt D tot M even groot moet zijn als de afstand van punt D tot punt R op de cirkel. Oftewel ik kan de vraag helemaal oplossen alleen zonder gebruik te maken van de stelling van Thales, maar hoe moet het nu mét die stelling?
(ik heb een tekening gemaakt voor de duidelijkheid, maar die krijg ik er niet bij geplakt?!)
Alvast ontzettend bedankt!
Groetjes, Joske
Joske
Leerling bovenbouw havo-vwo - maandag 18 april 2005
Antwoord
Op een bepaald 'moment' heb je de volgende situatie:
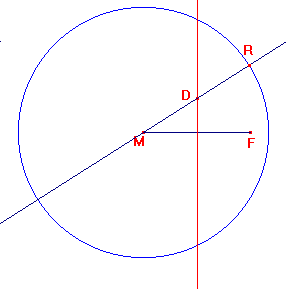
Je weet dat (vanwege de genoemende afstanden) dat M, F en R op een cirkel liggen met D als middelpunt. Hoe vind je nu de plaats van R?
ÐMFR=90°!
Waarom? De stelling van Thales!
Help dat?

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 23 april 2005
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2025 WisFaq - versie 3
|










