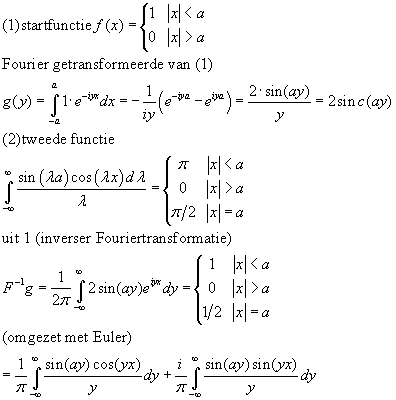|
|
|
\require{AMSmath}



Integreren van sin(x)/x met behulp van fouriertransformatie
Op school heb ik gezien hoe je de sinc functie van -•tot +• kan integreren mbv fouriertransformaties. Nu heb ik dit eens herbekeken en heb ik toch enkel vragen. Hopelijk kunt u mij helpen.
Eerst transformeren we de fuctie f(x) die is 1 als |x| a en 0 als |x| a en 0 als |x| a a
getransformeerde is g(y) (zie figuur)
met deze uitkomst zou je dan de volgende integraal moeten kunnen uitwerken...maar dat lukt mij niet. Met het reŽel deel van deze laatste stap zou je dan de integraal van de sinc functie kunnen bepalen.
alvast bedankt voor uw moeite.
Ik hoop dat iemand mij kan helpen
Wim De
Student Hoger Onderwijs BelgiŽ - donderdag 31 maart 2005
Antwoord
dag Wim,
Eerst even wat slordigheidjes in jouw uitwerking wegwerken.
In de startfunctie f(x) ben je de waarde 1/2 voor |x|=a vergeten (later wel weer goedgemaakt)
Ten tweede is in de derde regel de laatste stap een a vergeten. (moet zijn: 2a∑sinc(ay))
Verder heb je in de regel van de inverse getransformeerde de sin gezet in plaats van de sinc.
Maar nu het antwoord op je vraag:
Het reŽle deel van de Euler-uitwerking heeft in de teller staan: sin(ay)cos(yx).
Kies nu (voor het speciale geval dat we willen aantonen) voor x en voor a beide de waarde 1.
Dan staat hier in die teller dus juist 1/2sin(2y)
Dus de integrand wordt sin(2y)/2y
Verder weet je al de uitkomst van dit reŽle deel, namelijk 1/2
Dan moet het verder lukken, hoop ik, anders hoor ik het nog wel.
groet,

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 3 april 2005
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2025 WisFaq - versie 3
|








 a en 0 als |x|
a en 0 als |x| a
a