|
|
|
\require{AMSmath}



Verdelen van een rechte hoek
Hallo,
Ik ben construktie-plaatwerker en maak wel eens segmentbochten,over het optekenen hiervan heb ik een vraag.
Is het mogelijk om 1/4 cirkel in 4 gelijke en 2 halve delen(te beginnen met 1 halve, dan 4 hele en daarna nog 1 half deel)snel en nauwkeurig met de passer uit te zetten, of ben ik gebonden aan de gradenboog??
Als met de passer mogelijk is en u een antwoord wil geven graag een verduidelijkende tekening.
Bij voorbaat hartelijk dank.
A.Stam
Iets anders - maandag 17 januari 2005
Antwoord
We delen de rechte hoek dus op in vijf delen van elk 18°. Het laatste deel splitsen we dan in hoeken van elk 9°.
Het komt dan neer op het construeren van een regelmatige vijfhoek (en gelukkig kan dat met passer EN liniaal).
Hieronder staat de tekening.
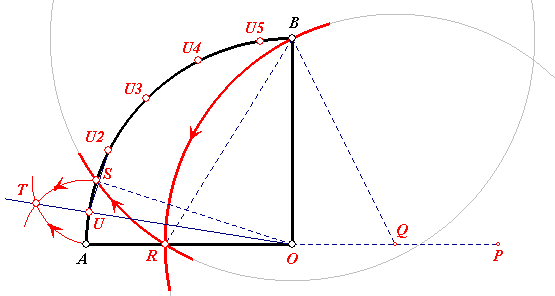
De rechte hoek wordt bepaald door de punten A, O, B.
De constructiestappen:
- Punt P op het verlengde van AO met AO = OP.
- Punt Q is het midden van OP.
- Cirkel met middelpunt Q en straal QB; genoteerd als (Q, QB).
- Snijden van die cirkel met AO geeft het punt R.
- Cirkel (B, BR) en snijden daarvan met boog AB geeft S.
Nu is hoek SOA = 18°.
- Cirkel (S, SA) en cirkel (A, AS) snijden elkaar in T.
- De lijn OT snijdt boog AB in U.
Nu is hoek AOU = 9°
De constructie van de overige deelpunten, U2, ..., U5 spreekt nu, denk ik, voor zichzelf.
De vraag is echter of eea. met een gradenboog toch niet nauwkeuriger (en sneller) is.

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 20 januari 2005
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2025 WisFaq - versie 3
|










