|
|
|
\require{AMSmath}



Re: Goniometrische vergelijking
Ik heb wat geprobeerd nadat ik mijn vraag had gesteld; ik kom uit op het volgende:
cos 2 x = cos x +2
2 cos2x - 1 = cos x +2
2 cos2x - cos x = 3
2 cos2x - cos x -3 = 0
stel p = cos x, dan:
2p2 - p - 3 = 0
D = (-1)2 - 4*2*-3 = 25
p = (-(-1) + Ö(25))/ 2*2 = 1,5 of
p = (-(-1) - Ö(25))/ 2*2 = -1
p = cos x, dus:
cos x = 1,5 of cos x = -1
kan niet of cos x = cos p
x = p + k*2p of x = -p + k*2p
Het antwoordenboek geeft het volgende als antwoord:
x = k*2p of x = -2/3p + k*2p of x = 2/3p + k*2p
Is mijn antwoord toch fout? Hoe komt het antwoordenboek op zo'n antwoord?
Alvast dank.
Hans
Leerling bovenbouw havo-vwo - woensdag 1 december 2004
Antwoord
Eh... ik zou van cos(x)=-1 gewoon als oplossing geven:
x=p+k·2p met kÎ
Ter controle (geheel overbodig natuurlijk) even in mijn GR gezet...
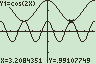
Mij lijkt je oplossing (op die rare -p-kronkel na dan) wel in orde!? Ach antwoordenboekjes... ze roepen soms maar wat...

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 1 december 2004
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2025 WisFaq - versie 3
|








 Dit is een reactie op vraag 30751
Dit is een reactie op vraag 30751 



