|
|
|
\require{AMSmath}



Maple: raaklijn aan een functie met y en x
Hallo,
Zit hier met een klein probleempje. Moet deze vraag oplossen met maple:
Bepaal de raaklijn aan de duivelskromme
y^2(y^2-4) = x^2(x^2-5)
in het punt (0,-2) en teken de duivelskromme.
Nu heb ik even dit gedaan:
 f:=x- f:=x- (y^2)*((y^2)-4)=(x^2)*((x^2)-5); (y^2)*((y^2)-4)=(x^2)*((x^2)-5);
2 / 2 \ 2 / 2 \
f := x - y \y - 4/ = x \x - 5/ y \y - 4/ = x \x - 5/
 f(x); f(x);
2 / 2 \ 2 / 2 \
y \y - 4/ = x \x - 5/
 implicitdiff(f(x),y,x); implicitdiff(f(x),y,x);
3
-2 x + 5 x
- -----------
3
2 y - 4 y
 h:=x- h:=x- -(-2*x^3+5*x)/(2*y^3-4*y); -(-2*x^3+5*x)/(2*y^3-4*y);
3
-2 x + 5 x
h := x - - ----------- - -----------
3
2 y - 4 y
 h(x); h(x);
3
-2 x + 5 x
- -----------
3
2 y - 4 y
 h(0,-2); h(0,-2);
0
Maar dan zou de rc=0 worden en dat zou eventueel wel kunnen maar via y=ax+b krijg je dan -2=0x+b b=-2. -2=-2. Lijkt me dat dit een fout antwoord is.
Iemand die weet of er misschien een betere functie in maple zit (begin er pas net mee) of even een betere stappenvolgorde heeft?
Bvd
Bastij
Student universiteit - maandag 18 oktober 2004
Antwoord
Ik denk dat Maple het wel goed doet.
Je krijgt via implicitdiff de functie
h(x,y) = x(2x2-5)/2y(y2-2)
met h(0,-2) = 0
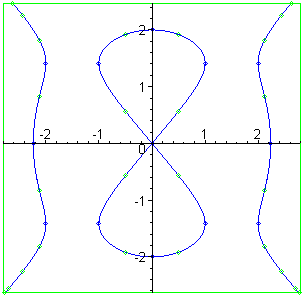
Als je de duivelskromme tekent met
 with (algcurves): with (algcurves):
 f:=(y^2)*((y^2)-4)-(x^2)*((x^2)-5): f:=(y^2)*((y^2)-4)-(x^2)*((x^2)-5):
 plot_real_curve(f,x,y); plot_real_curve(f,x,y);
dan blijkt dat die kromme inderdaad in (0,-2) een horizontale raaklijn (met vergelijking y = -2) heeft.

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 18 oktober 2004
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2025 WisFaq - versie 3
|








 f:=x-
f:=x-

