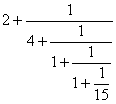WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Raderwerk berekeningen

geachte heer/mevrouw,

ik zit met een probleem, ik ben van plan een planetarium te vervaardigen maar ik kom niet uit de berekeningen.
ik zal u in een notendop uitleggen wat mijn probleem is.

je hebt twee planeten die met een verhouding (ten opzichte van elkaar) om de zon heen draaien. de irrationale verhouding tussen de planeten is wel te vinden, dat is de tijd (in sec.) die de planeten er over doen om door hun meridiaan tegaan.

deze getallen zijn zo groot (en met meerdere decimalen) dat het in een uurwerk practies onuitvoerbaar word om het temaken.

Door middel van vereenvoudigen en een kettingbreuk is het mogelijk om een verhouding tussen de twee getallen tevinden die wel uit te voeren is maar toch dezelfde verhouding heeft (dat de planeten wel een hoge nauwkeurigheid verplatsen).

het probleem komt nu: ik weet niet hoe ik deze berekening moet uit voeren en de vraag was dus ook of u mij in deze zou kunnen helpen, en mij de werking van kettingbreuken met deze toepassing kunt uit leggen.

mochten er onduidelijkheden zijn over mijn vraag of zou u meer informatie nodig hebben dan kunt u gerust kontakt met mij opnemen.
Ik hoop dat u me met dit probleem kunt helpen en ik hoor graag spoedig van u.

dank bij voorbaat,
Jos Wi
Leerling mbo - woensdag 15 september 2004

Antwoord

Ik begrijp van je vraag het volgende:
Je hebt een verhouding van twee 'rare' getallen.
Je wilt deze zo goed mogelijk benaderen met twee gehele getallen zo, dat je deze gehele getallen als aantallen tanden van twee raderen kunt nemen.

Je zou dat zo kunnen doen.
Stel (ik noem maar wat) de verhouding is $\pi$:√2.
Bereken nu een decimale benadering van $\pi$/√2=2.221441469.
Bereken nu
2.221441469-2=.221441469 (onthoud op een briefje die 2)
Bereken nu 1/.221441469=4.515865995.
Bereken nu 4.515865995-4=.515865995 (onthoud op een briefje die 4)
Bereken nu 1/.515865995=1.938487922.
Trek hier 1 vanaf (1 op een briefje) en weer 1/...
Zo ga je even door.
De getallen die je hebt opgeschreven vormen de getallen van de kettingbreuk.
In ons geval b.v. : 2 4 1 1 15....(reken dat even zelf na)
Dat betekent dat je $\pi$/√2 bij benadering te schrijven is als:

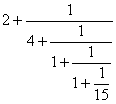
We gaan nu terug rekenen:
1+1/15=16/15
1+1/(16/15)=1+15/16=31/16
4+1/(31/16)=4+16/31=140/31
2+1/(140/31)=2+31/140=311/140
311/140=2.221428571 terwijl $\pi$/√2=2.221441469.
Dit klopt dus tot op de 4e decimaal.
Je ziet dat 311/140 een redelijke benadering is van $\pi$/√2.

Samengevat: bepaal eerst een decimale benadering door de twee getallen op elkaar te delen.
Bepaal vervolgens de kettingbreukontwikkeling.
Reken daarna terug naar een gewone breuk.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 15 september 2004