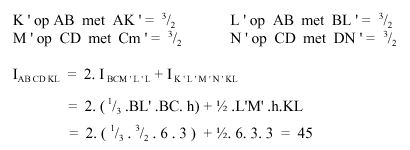|
|
|
\require{AMSmath}



Examenopgave 2000-I opgave 3
Sinds ik best veel moeite heb met meetkunde ben ik veel examenopgaven aan het oefenen. Mijn probleem ligt bij opgave 3 van het eindexamen van 2000 uit het eerste tijdvak (oude stijl)
Helaas is het antwoord van vraag 9 dermate beknopt dat ik niet weet wat ze doen. Kunnen jullie mij helpen?
Wouter
Leerling bovenbouw havo-vwo - woensdag 5 mei 2004
Antwoord
Ok, hier staat de opgave:
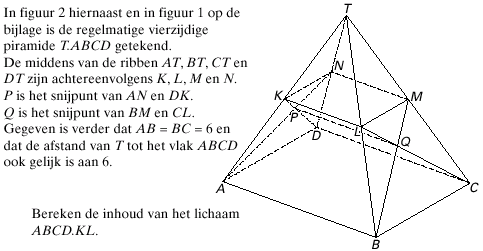
Als je de inhoud wil berekenen van ABCD.KL dan verdeel je dat lichaam in 'bekende' lichamen. In dit geval dus een prisma en twee piramides.
Dit doen ze door de volgende punten toe te voegen:
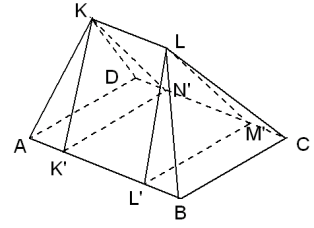
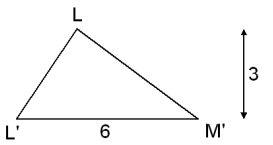
Laten we even kijken naar het grondvlak:
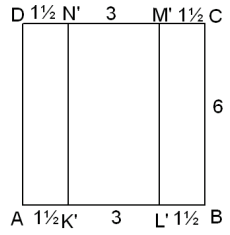
Eerst de inhoud van de piramide BCM'L'.L Het grondvlak heeft een oppervlakte van 9 en de hoogte is 3. Dus de inhoud van één zo'n piramide is 1/3·9·3=9. Daar heb je er twee van, dus inhoud piramides is 18.
De inhoud van het prisma KK'N'.LL'M'. Het grondvlak (LL'M') heeft een oppervlakte van 1/2·6·3=9
Dus de inhoud van het prisma is 9·3=27
Totale inhoud van ABCD.KL is 18+27=45
Dit kan je dus ook allemaal uit het antwoord halen:
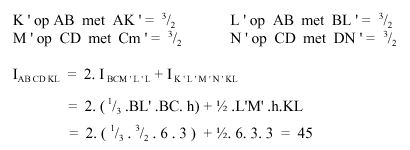
Vooral een kwestie van schetsen maken, goed lezen en goed letten op de plaats en naamgeving van de punten die je toevoegt. Hopelijk heb je er iets aan.

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 5 mei 2004
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2025 WisFaq - versie 3
|