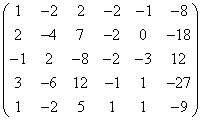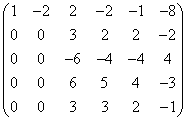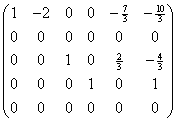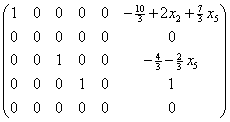|
|
|
\require{AMSmath}



Stelstel van 5 vergelijkingen met 5 onbekenden
Ik moet volgend stelsel oplossen, maar het lukt me niet. Kan iemand me helpen? (Ik zette die cijfers die in subscript moeten tussen haakjes, deze browser ondersteunt de onderstaande karakters blijkbaar niet)
Bedankt!
x1-2x2+2x3-2x4-x5=-8
2x1-4x2+7x3-2x4=-18
-1x1+2x2-8x3-2x4-3x5=12
3x1-6x2+12x3-x4+x5=-27
x1-2x2+5x3+x4+x5=-9
Manu
Student hbo - donderdag 15 april 2004
Antwoord
Hoi Manu,
ik heb begrepen dat je dit stelsel met matrices wilt oplossen maar vastgelopen bent met de methode van Gauss-Jordan.
Eerst de coefficienten matrix:
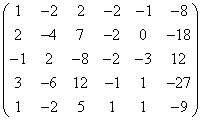
Vegen met de eerste rij levert:
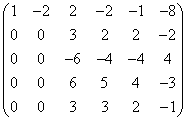
Omdat nu gelijk kolom 1 en 2 zijn geveegd kan het stelsel alleen oplossingen hebben als x2 vrij gekozen kan worden, maar dan moet er een rij met louter nullen ontstaan.
Dit kan door de helft van rij 3 op te tellen bij rij twee. Gecombineerd met zorgen dat het derde element van rij 3 1 wordt levert dit:

Verder systematisch werken met de methode van Gauss Jordan levert dan uiteindelijk:
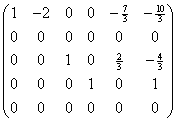
Ook de 5e rij blijkt nu louter nullen te bevatten, dus ook x5 kan vrij worden gekozen.
x2 maal kolom 2 van kolom 6 aftrekken, x5 maal kolom 5 van kolom 6 aftrekken en kolom 2 en kolom 5 nul maken levert:
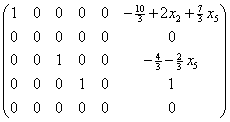
Conclusie: de oplossing van het stelsel is:
x1=-10/3+2x1+7/3x5
x2=x2
x3=-4/3-2/3x5
x4=1
x5=x5

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 17 april 2004
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2025 WisFaq - versie 3
|