WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

De stelling van Graaf van Buffon

Wat is de formule voor de verkleining per hoekvergroting. Hoe veel kleiner worden de verkleiningen dus als er meer hoeken komen.

Weet iemand een probleem dat te maken heeft met de stelling Graaf van Buffon.

Nadere toelichting:

Met de graaf van Buffon verbindt je de middens van zijden van een veelhoek met elkaar. Er ontstaat dan een nieuw figuur in de oude, waarvan de omtrek en het oppervlak een bepaalde verkleining heeft ten opzichte van de oude. Ik zou graag willen weten of jullie kunnen uitleggen wat de formule is voor de verkleining van het oppervlak en de omtrek ten opzichte van het orgineel. Ik zou ook graag willen weten hoe deze functie verandert als je een steeds grotere veelhoek neemt (meer hoeken). En zijn er ook toepassingen voor de graaf van Buffon?
Menno
Leerling bovenbouw havo-vwo - woensdag 4 februari 2004

Antwoord

Voor alle driehoeken bestaat er zulke vaste verhoudingen, zie: Stelling van Graaf van Buffon.

Of er voor willekeurige vierhoeken ook zulke vaste verhoudingen bestaan heb je misschien zelf al ontdekt. Bekijk anders onderstaand plaatje eens goed:

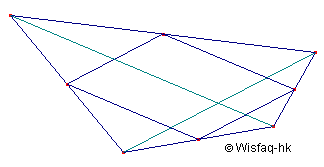
We gaan nu vijfhoeken onderzoeken.
Hieronder staat een applet die een Cabri-tekening laat zien.
Cabri is een meetkundeprogramma dat ook op school aanwezig is.
In de applet hieronder is een willekeurige vijfhoek getekend in blauw.

Applet werkt niet meer.
Download het bestand.

Links en rechts staan de oppervlakte en omtrek van de willekeurige vijfhoek en zijn verkleiningen.
Je kunt de hoekpunten van de willekeurige vijfhoek verslepen. Onderzoek eens of er nu van die vaste verhoudingen bestaan.
Ook staat een regelmatige vijfhoek getekend. Je kunt de hoekpunten van de regelmatige vijfhoek verlepen naar de hoekpunten van de regelmatige veelhoek. Hoe zit het nu?

Voor een regelmatige veelhoek is ook het mogelijk door berekening na te gaan of en zo ja welke verhoudingen er zijn. Bijvoorbeeld een regelmatige vijfhoek:

Het antwoord kun je vinden door de verhouding van de rode en blauwe lijnstukjes uit te rekenen. Als je deze kunt berekenen kun je de formules voor andere regelmatige veelhoeken ook wel vinden.

Over een ander probleem dat te maken heeft met het probleem van graaf de Buffon heb ik niet zoveel ideeen.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 8 februari 2004

Re: De stelling van Graaf van Buffon