|
|
|
\require{AMSmath}



De bomen van Pythagoras: dimensie
Wij moeten voor school een PO maken. We hebben voor het onderwerp Fractals gekozen. We zitten alleen met een probleempje.
Is het namelijk mogelijk om de dimensie van de bomen van Pythagoras uit te rekenen? Zo ja, dan willen wij graag weten hoe.
Alvast bedankt
Paul v
Leerling bovenbouw havo-vwo - zaterdag 31 januari 2004
Antwoord
Beste Paul,
Het begrip dimensie werkt voor fractals als volgt:
Stel je vergroot de figuur met een factor S, en in die vergrote figuur passen precies N van de oorspronkelijke fractals, dan is de D zodat SD = N de dimensie. Ofwel D = log N/log S.
Zie ook Mathematical Interpretation of Fractal Dimension.
Een probleem bij de Pythagoras-boom is allereerst dat hij zichzelf overlapt. Maar dat we vergeten eens even. Dan is er nóg een probleem.
Laten we eens beginnen met een Pythagoras-boom met een 45-45-90 driehoek als uitgangspunt. In die boom zitten twee exact gelijke verkleiningen verborgen. (In de figuur moet je de Pythagorasboom natuurlijk in oneindig ver doorgevoerd denken. Om praktische redenen heb ik dat niet gedaan).
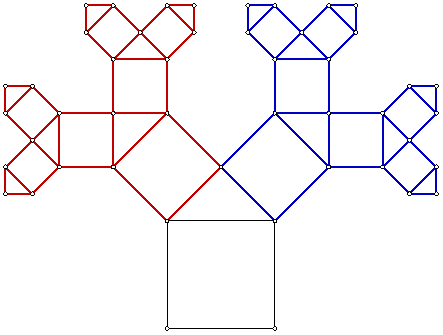
De grote Pythagorasboom is een vergroting van de twee kleinere bomen met een factor  2, dus S= 2, dus S= 2. Maar de twee kleinere bomen bedekken niet héél de grote boom, de onderste vierkant en driehoek blijven vrij. 2. Maar de twee kleinere bomen bedekken niet héél de grote boom, de onderste vierkant en driehoek blijven vrij.
Ik denk dat we dat in dit geval wel mogen verwaarlozen. Van elke generatie hebben de driehoeken en vierkanten samen dezelfde oppervlakte als de driehoek en vierkant van generatie 0, diegene waarmee we begonnen. De totale oppervlakte is dus oneindig. Dan kunnen we die eerste driehoek en vierkant wel verwaarlozen en stellen dat N=2. Maar helemaal 100% zuiver is het niet.
Met N=2 en S= 2 vinden we dat D=2. Dus de dimensie van de 45-45-90 Pythagorasboom is dezelfde als van een gewone vlakke figuur. 2 vinden we dat D=2. Dus de dimensie van de 45-45-90 Pythagorasboom is dezelfde als van een gewone vlakke figuur.
Hoe zou dat nou gaan met een scheve Pythagorasboom?
We gaan eens uit van een boom waarvan een van de niet rechte hoeken gelijk is aan A. We nemen eens de lengte van het basisvierkant gelijk aan 1. Dan zijn de twee rechthoekzijden van de driehoek sin(A) en cos(A).
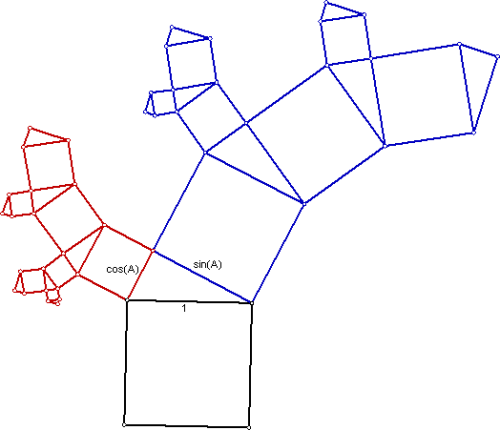
De twee delen die nu samen (bijna) de grote boom vormen hebben niet dezelfde verkleinde factor. Als we eens van de rode tak uitgaan, dan is de hele figuur vergroot met een factor S=1/cos(A).
N is wat moeilijker. De blauwe tak is met een factor tan(A) vergroot ten opzichte van de rode tak. Met bovenstaand dimensieverhaal telt die dus mee met een factor (tan(A))D. Dus we moeten N maar nemen als N = 1 + (tan(A))D.
Dus we moeten D zoeken zodat (1/cos(A))D = 1 + (tan(A))D. Vermenigvuldig alles met (cos(A))D en je krijgt 1 = (cos(A))D + (sin(A))D. Hieruit halen we dat D=2 vanwege een beroemde goniometrische formule!

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 1 februari 2004
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2025 WisFaq - versie 3
|









 2, dus S=
2, dus S=

