|
|
|
\require{AMSmath}



Afgeleide functie van f(x)=x·sin(x)+cos(x)
Gegeven is de functie f(x)=x·sin(x)+cos(x)
a. bereken de waarde van de afgeleide functie bij x=1.
Is dit goed?
f(x)'= 1·sin(x)+x·cos(x)-sin(x)=x·cos(x)
f(x)'= 1·cos(1) = 0.5
b. stel de raaklijn op in het punt bij x=0.
Hoe stel ik een raaklijn op?
Geert-
Student hbo - vrijdag 17 oktober 2003
Antwoord
Beste Geert-Jan,
a) f(x)=x·sin(x)+cos(x) is een som, waarbij de termen x·sin(x) en cos(x) zijn. De afgeleide van een som is de afgeleide van de termen. Dus f'(x) = (x·sin(x))' + (cos(x))'
Om (x·sin(x))' te bepalen moet je gebruikmaken van de productregel, die zegt (f·g)' = fg' + gf', hier toegepast (x·sin(x))' = x·cos(x) + sin(x)·x' = x·cos(x) + sin(x).
Je moet dus ook weten dat x' = 1 en dat (sin(x))' = cos(x).
Maar je weet ook dat (cos(x))' = -sin(x), dus (x·sin(x))' + (cos(x))' = x·cos(x) + sin(x) - sin(x) en dat is x·cos(x).
Je hebt de functie dus goed afgeleid, maar f'(1) is bij benadering 0,5403023059, en niet precies 0,5 zoals dat wel uit jouw antwoord kan opgevat worden.
b) Dan de vergelijking opstellen van de raaklijn in het punt x=0. Dit wordt ookwel de linearisering in een punt genoemd en er is een standaardformule voor.
De linearisering van f in a is L(x)=f(a)+f'(a)·(x-a)
Hier is a=0, f(0)=1 en f'(x)=x·cos(x), dus f'(a) = f'(0) = 0.
Dus L(x) = 1 + 0·(x - 0) Û L(x) = 1.
In een grafiekje krijgen we
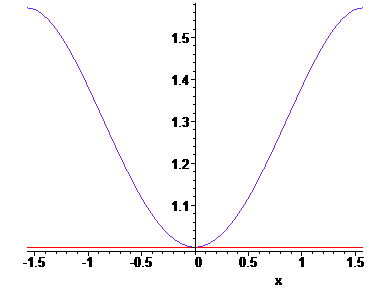

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 17 oktober 2003
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2025 WisFaq - versie 3
|










