WisFaq!

Loading jsMath...

De digitale vraagbaak voor het wiskundeonderwijs

HOME

\require{AMSmath}

Afleiden van de somregel van sinus

Hoe kan ik van de regel sin (a+b)= sin a·cos b+ cos a·sin b de formules sin(2a) en sin(a/2) afleiden. Alvast bedankt, roeten
Philip
Leerling bovenbouw havo-vwo - zondag 25 mei 2003

Antwoord

Hoi,

Formule afleiden voor sin(\alpha+\beta) = sin\alpha·cos\beta + cos\alpha·sin\beta

Beschouw onderstaande rechthoek

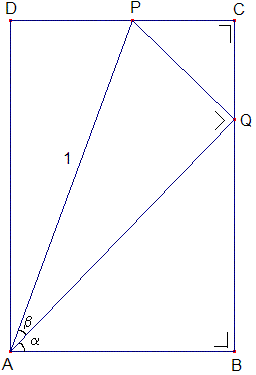
P en Q zijn zo gekozen dat \angleAQP = 90° en AP = 1.

\anglePQC = \alpha, want \angleBQA = 90° - \alpha en \angleBQC = 180° (gestrekte hoek) \Rightarrow \anglePQC = 180°-\angleBQA - \angleAQP = 180° - (90° - \alpha) - 90° = \alpha.

\angleAPD = \alpha+\beta, dat zou je kunnen bewijzen a.d.h.v. een Z-hoek, want AB // DC \Rightarrow \angleBAP = \angleDPA (je zou 't ook anders kunnen aanpakken: \angleADP = 90°, \angleDAP = 90° - (\alpha+\beta) \Rightarrow \angle DPA = 180° - 90° - (90° - (\alpha+\beta)) = \alpha+\beta.

Nu gaan we 'n schema invullen (hou rekening met AP = 1)!

In de rechthoek geldt dat AD = BQ + QC. A.d.h.v. de tabel kunnen we laten zien dat sin(\alpha+\beta) = AQ·sin\alpha+PQ·cos\alpha, want sin\alpha=^BQ/_AQ en cos\alpha=^CQ/_PQ en sin(\alpha+\beta) = AD.

Invullen levert: AD = AQ·^BQ/_AQ + PQ·^CQ/_PQ \Rightarrow AD = BQ + CQ.

We kunnen die AQ en PQ ook vervangen. Krijgen we sin(\alpha+\beta) = cos\beta·sin\alpha + sin\beta·cos\alpha en aangezien bij de vermenigvuldiging de factoren van plaats mogen ruilen (want 4·3 = 3·4 bijvoorbeeld) mogen we ook schrijven sin(\alpha+\beta) = sin\alpha·cos\beta+cos\alpha·sin\beta.

Om de regel van cos(\alpha + \beta) te bewijzen kun je gebruikmaken van het feit dat PD = AB - PC, en op analoge wijze krijg je dat cos(\alpha+\beta) = cos\alpha·cos\beta - sin\alpha·sin\beta (we noemen deze formules de somformules)

Je kunt nu ook op de verschilformules hieruit afleiden, maar dan moet je wel weten dat cos(-t) = cos(t), sin(-t) = -sin(t).

Formule afleiden voor sin(2\alpha)

sin(2\alpha) = sin(\alpha+\alpha). Dus gewoon \beta vervangen door \alpha in bovenstaande formule.

sin(\alpha+\alpha) = sin\alpha·cos\alpha + sin\alpha·cos\alpha = 2sin\alpha·cos\alpha.

cos(2\alpha) gaat analoog, je krijgt cos²\alpha - sin²\alpha als uitkomst.

Formule afleiden van sin(¹/₂\alpha)

Vervang in bovenstaande formule \alpha door ¹/₄\alpha.

sin(2·¹/₄\alpha) = 2sin(¹/₄\alpha)·cos(¹/₄\alpha)

Ik hoop dat het zo wat duidelijker is geworden, zo niet dan hoor ik het wel,

Groetjes,

Davy.
Zie Meer informatie...

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 25 mei 2003

Re: Afleiden van de somregel van sinus