De standaardafwijking berekenen bij de normaal verdeling met je GR
Hallo, ik snap de volgende opdracht niet:
Een munt van 2 euro heeft een diameter van 25.75 mm. Een automaat is nauwkeurrig afgesteld, dat een munt van 2 euro wordt geweigerd als deze meer dan 0.40 mm van het gemiddelde afwijkt.
In de automaat worden 1000 willekeurige 2 euro munten gedaan. De automaat weigert daarvan: 3 munten met een te kleine en 3 munten met een te grote diameter.- Bereken op grond van deze gegevens de standaardafwijking van de 2 euro munt (in 2 decimaal)
Ik wil graag weten hoe je dat moet doen met de grafische rekenmachine, waarschijnlijk met normalcdf, maar verder snap ik het niet...
berend
Leerling bovenbouw havo-vwo - dinsdag 25 mei 2004
Antwoord
Aangenomen dat de diameter van een twee-euromunt normaal verdeeld is dan weten we:
$\mu$=25,75
$\sigma$=?
0,3% van de munten wijkt meer dan 0,40 mm af van het gemiddelde (x=26,15)
M.b.v. de standaard normale verdeling
We weten dat $\Phi$(z)=0,997
Met je GR kan je de bijbehorende z-waarde vinden:
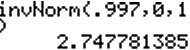
z$\approx$2,748
Invullen in de standaard-formule levert:
$
\eqalign{
& {\text{2}}{\text{,748 = }}\frac{{{\text{26}}{\text{,15 - 25}}{\text{,75}}}}
{\sigma } \cr
& {\text{2}}{\text{,748 = }}\frac{{{\text{0}}{\text{,40}}}}
{\sigma } \cr
& \sigma = \frac{{{\text{0}}{\text{,40}}}}
{{{\text{2}}{\text{,748}}}} \approx 0,15 \cr}
$
Grafisch
Vul in het grafiekenscherm in:
Y1=normalcdf(25.35,26.15,25.75,X)
Y2=0,994
Window [0,1]x[0,1]
...en dan Calc/Intersect geeft X=0,1455... dus $\rho\approx$0,15

dinsdag 25 mei 2004
|
 ©2004-2024 WisFaq
©2004-2024 WisFaq
|