WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Oppervlakte regelmatige n-hoek

Ik ben hopeloos aan het zoeken naar een formule om de oppervlakte van een gelijkzijdige zeshoek, achthoek, twaalfhoek en zestienhoek te berekenen. Jammer genoeg vind ik hier heel weinig over.
Saskia
Iets anders - zondag 3 februari 2002

Antwoord

Het is mogelijk voor een willekeurige n-hoek een formule voor de oppervlakte af te leiden (zelfs met elementaire wiskunde).

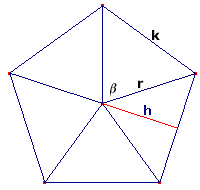
De hoekpunten van zo'n n-hoek liggen op een cirkel met straal r. Deze n-hoek bestaat uit n gelijkbenige driehoeken met basis k, hoogte h en tophoek ß.

De oppervlakte van één zo'n driehoek is ½·k·h

h=r·cos(ß/2)

k=2·r·sin(ß/2)

Opp.(driehoek)=½·2·r·sin(ß/2)·r·cos(ß/2)=r²·sin(ß/2)·cos(ß/s)=¹/₂·r²·sin(ß)

Opp.(n-hoek)=¹/₂·n·r²·sin(ß)

ß=360°/n

Opp.(n-hoek)=¹/₂·n·r²·sin(360°/n)

Daarmee kan je voor een willekeurige n-hoek de oppervlakte uitrekenen.

Voor r=1 en n$\infty$ zou hier dan uit moeten komen...

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 3 februari 2002

klein | normaal | groot