Vraagstuk vierkantsvergelijkingen

ik heb 3 opgaven waar ik vast loop

opgave1:
bepaal de punten op de recht a (= y=3x-1) die op een afstand 2√10 liggen van het punt P(2,5).

mijn oplossing:
ik heb al ontdekt dat het punt op de grafiek ligt en probeerde met de afstandsformule voor 2 punten de 2 te zoeken punten te vinden. Maar weet niet hoe ik verder moet. Ik kom een vergelijking uit voor een cirkel, maar heb dit nog niet geleerd.

opgave 2:
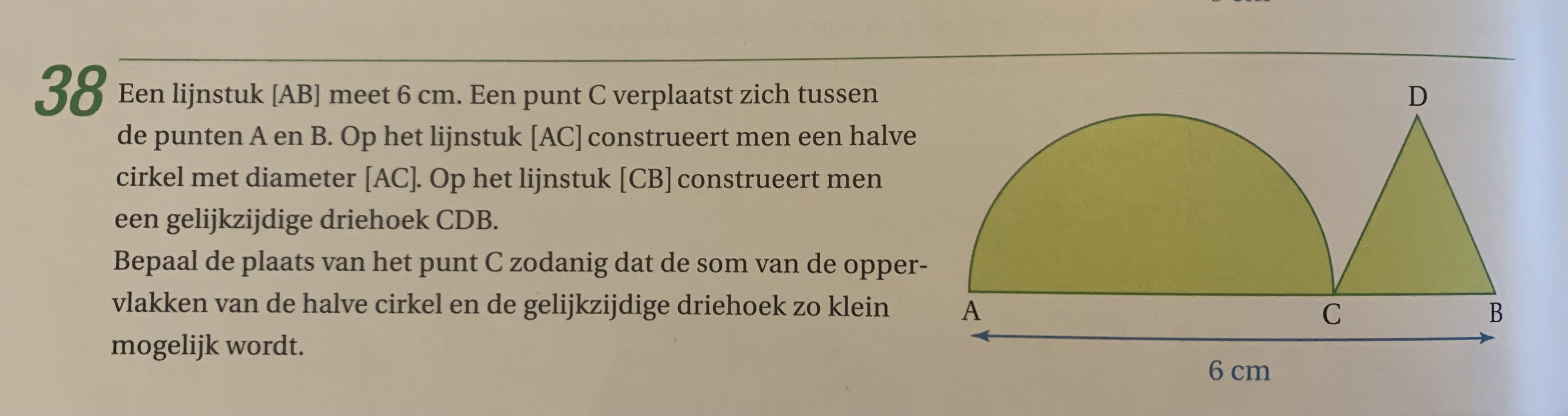
(zie foto 1)
oplossing:
a = AC, b = CB
ik heb al a+b=6 (om a of b gelijk te stellen)
en opp cirkel +opp driehoek, ((a/2)²* $\pi$ )/2+(b*(a/2))/2
om een of andere reden kom ik verkeerd uit.

opgave 3:
op elk van de zijden van een ruit met lengte van de diagonalen 6en 8 nemen we een punt zodanig dat de verkregen vier punten de hoekpunten zijn van een rechthoek waarvan de zijden evenwijdig zijn met de diagonalen van de ruit. Bepaal de afmetingen van de rechthoek zodanig dat zijn oppervlakte een maximum bereikt.

opl:
x= de lengte van grote basis ruit - lengte rechthoek basis
y= de lengte van de kleine basis ruit - lengte hoogte rechthoek
x/8=-y/6 (evenredigheid)
opp rechthoek= b*h= (8-2x)*(6+2y)

max
2de graad ASO - vrijdag 31 maart 2023

Antwoord

In alle gevallen kun je de ene variabele in de andere uitdrukken.

1. Het gaat om $(x-2)^2+(y-5)^2=40$, maar $y=3x-1$ dus je kunt daar $(x-2)^2+(3x-6)^2=40$ van maken en dat is een kwadratische vergelijking.

2. Je hebt $\frac\pi8a^2+\frac14ab$; vervang $b$ door $6-a$ en je hebt weer een kwadratische functie; nu moet je daar het minimum van bepalen.

3. Ook hier: je kun ook hier, met behulp van $x=-\frac43y$ of $y=-\frac34x$, een kwadratische functie van maken en daar het maximum van bepalen.

kphart
vrijdag 31 maart 2023

Re: Vraagstuk vierkantsvergelijkingen

©2001-2024 WisFaq