Oppervlakte exact berekenen

In één figuur staan de grafieken van de functies f(x)=√x en g(x)=(1/x√x) samen met de lijn l met vergelijking y = $\frac{1}{32}$x.

G is het gebied dat wordt ingesloten door de grafieken van f en g en de lijn l.

• Bereken exact de oppervlakte van het gebied G.

Hans B
Leerling bovenbouw havo-vwo - zondag 21 maart 2021

Antwoord

Hallo Hans,

Maak een schets. Dit hoeft niet op schaal, het gaat erom dat je ziet hoe de grafieken ten opzichte van elkaar liggen en wat precies het gebied G is. Zo'n schets ziet er zo uit:



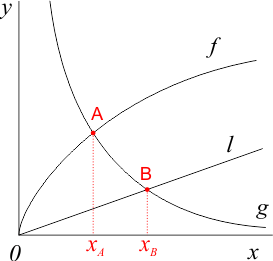
In de schets zie je dat gebied G wordt bepaald door f(x)-l voor x=0 tot x=x_A plus g(x)-l voor x=x_A tot x=x_B.

Dus:

• Bereken de x-coördinaten van de snijpunten A en B
  
• Integreer f(x)-y en g(x)-y tussen de aangegeven grenzen

Lukt het hiermee? Zo niet, stel dan gerust een vervolgvraag, maar laat dan wel zien wat je zelf hebt geprobeerd, zie de spelregels.

zondag 21 maart 2021

Re: Oppervlakte exact berekenen

©2001-2024 WisFaq