Oppervlakte benaderen

In een figuur staat een deel van de grafiek van f(x)=x√(25-x²) en de lijn y=3x.

1. Benader de oppervlakte van het gebied, dat wordt ingesloten door de grafiek van f en de positieve x-as met behulp van een Riemann-som met vijf deelintervallen. Rond je antwoord af op twee decimalen.
2. Door de grafiek van f en de lijn y=3x wordt een gebied G ingesloten. Geef de integraal waarmee je de oppervlakte van dit gebied kunt berekenen en bereken daarmee de oppervlakte van G in twee decimalen.
3. De functie f heeft een primitieve van de vorm p · (25-x²)^q. Bereken exact de waarden van p en q.

Hans B
Leerling bovenbouw havo-vwo - zondag 21 maart 2021

Antwoord

Bij a. kan deze tekening van een benadering met de ondersom misschien helpen.



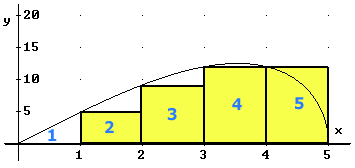
1e rechthoekje hoogte is $f(0)=0$
2e rechthoekje hoogte is $f(1)=2\sqrt{6}$
3e rechthoekje hoogte is $f(2)=2\sqrt{21}$
4e rechthoekje hoogte is $f(3)=12$
5e rechthoekje hoogte is $f(4)=12$

De breedte van de rechthoekjes is 1. Een benadering voor de oppervlakte onder de grafiek is de som van de 5 oppervlakten:

$
\sum\limits_{k = 0}^4 {f(k)} \approx {\text{38}}{\text{,06}}
$

Je zou natuurlijk ook naar de bovensom kunnen kijken. Moet je maar 's doen! Ik kom dan uit op:

$
\sum\limits_{k = 1}^5 {f(k)} \approx {\text{38}}{\text{,06}}
$

Dat lijkt wel hetzelfde...

Bij b. kan je, met je rekenmachine, een benadering vinden voor de integraal:

$
\int\limits_0^5 {{\text{x}}\sqrt {{\text{25 - x}}^{\text{2}} } } dx \approx 41,67
$

Bij c. is het handig om de zaak om te draaien. Bereken de afgeleide van:

$F(x) = p \cdot \left( {25 - x^2 } \right)^q$

Je kunt dan de waarden voor $p$ en $q$ bepalen. Dat moet kunnen...

Succes!

zondag 21 maart 2021

©2001-2024 WisFaq