Integraal met een functie in e-macht

hoi ik moet een oppervlakte bepalen: f(x)= e^1+2x en g(x)= e^1-x en de rechten zijn x = -2, x = 1 en y= 0

ik heb het geprobeerd en ik kom e^1+ e^-3 - e^0 + e^1 uit. maar dit klopt niet. ik zou -3e + e^-1 + (1/2)e^-3 + (1/2)e^3+1 moeten hebben. hoe kan ik dit oplossen? en vanwaar komt die 1/2?

elke
3de graad ASO - dinsdag 19 januari 2021

Antwoord

Hallo Elke,

Er ontbreken haakjes in je notatie. Hieronder zie je wat ik denk dat je bedoelt.

Eerst maar eens de primitiven bepalen:



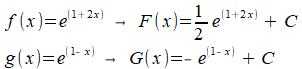
De factor ¹/₂ in de primitieve F(x) heeft te maken met de kettingregel. Wanneer je de afgeleide van F(x) bepaalt, moet je de oorspronkelijke functie f(x) weer terugkrijgen. In de exponent van f(x) komt een factor 2 voor, vanwege de kettingregel volgt dan een vermenigvuldiging met 2. De factor ¹/₂ in F(x) zorgt ervoor dat je uitkomt op de juiste afgeleide.
Om dezelfde reden vind je een min-teken in de primitieve G(x).

De grafieken van f(x) en g(x) snijden elkaar in (0, e). Voor x$<$0 ligt de grafiek van g(x) boven de grafiek van f(x), voor x$>$0 is dit andersom. Links van de y-as vind je de gevraagde oppervlakte met F(x) tussen de grenzen x=-2 en x=0. Rechts van de y-as neem je G(x) tussen x=0 en x=1.

Dan is het een kwestie van zorgvuldig uitwerken:

Links van de y-as:



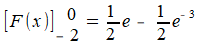
Rechts van de y-as:



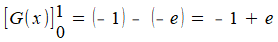
Optellen van de resultaten levert je de gevraagde oppervlakte:



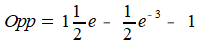
Ik kom uit op een ander resultaat dan jij aangeeft. Misschien bedoel je toch iets andere functies, of heb je een typfout gemaakt bij het overnemen van het antwoord? Ik kan natuurlijk ook een vergissing hebben gemaakt, maar na enkele keren narekenen vind ik toch mijn uitkomst.

woensdag 20 januari 2021

Re: Integraal met een functie in e-macht

©2001-2024 WisFaq