Lengteberekening van conische staaf dmv integreren

Beste,

Ik heb in de loop van mijn oefening een deel waar ik vastzit, niet omdat ik de oefening niet snap maar omdat ik een fout maak bij het integreren
De integraal is van 0 - 150
$\to$integr(0tot₁₅0)= (130/(21000·Pi·((12.5-0.05x)²)/4) )dx

Ik moet dan gebruik maken van een hulpvariabele, ik schrijf eerst op wat ik al heb.
(130·4/(21000·Pi))integr(0tot₁₅0) = dx/((12.5-0.05x)²)

met hulpvariabele u = 12.5-0.05x
du = 0-0.05 dx
dx = du/(-0.05)

dus als ik deze hulpvariabele invoeg krijg ik dit

(130·4/(21000·Pi)) integr(0tot₁₅0) = du/(-0.05·u²)
(130·4/(21000·Pi)) integr(0tot₁₅0) = (u^-2 · du)/ -0.05

nu haal ik deze 0.05 nog naar voor

(130·4/(21000·Pi·0.05))integr(0tot₁₅0) = (u^-2 · du)/ -1

maar nu zit ik echter vast, in de uitwerking van de leerkracht, wordt deze u^-2 $\to$ u^-1 tijdens het integreren. kunt u dit eens overzichtelijk verklaren alstublieft ?

Coppen
Student Hoger Onderwijs België - dinsdag 24 mei 2016

Antwoord

Hallo Arne,

Je bent tot hier gekomen:



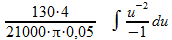
Dit kan je ook schrijven als:



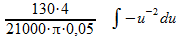
Je kent vast de basisregel voor de integraal van een machtsfunctie:



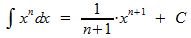
In woorden: de macht met 1 ophogen, en delen door deze nieuwe macht.
Nu moet je zorgvuldig invullen: de macht van u was -2, na ophogen wordt dit -1 (misschien dacht je dat dit -3 zou worden, een veel gemaakte vergissing). Ook moet je delen door deze -1, zodat je krijgt:



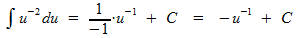
Samen met het min-teken dat al in jouw oorspronkelijke integraal stond, kom je dus uit op:



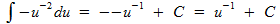
OK zo?

dinsdag 24 mei 2016

©2001-2024 WisFaq