Afgekeurde koffiezetters

Een bedrijf van huismerken koopt graag afgekeurde partijen koffiezetapparaten op van fabrikanten. Daarna worden deze apparaten van een nieuwe merknaam voorzien en op de markt gebracht.

Het bedrijf koopt de koffiezetters bij twee leveranciers. Namelijk 60% bij Electronics en 40% bij Phitronics. Van leverancier Electronics is bekend dat 10% van de apparaten niet goed is, bij Phitronics is 30% niet in orde.

Er is een nieuwe partij binnengekomen. Door slordig optreden van een magazijnbediende is niet meer te achterhalen of deze van Electronics of Phitronics is. Men neemt een steekproef van 20 van die apparaten. Deze worden uitvoerig getest. Vastgesteld wordt dat twee van die apparaten niet deugen.

Vraag a
Hoe groot is de kans op twee defecten als we vooraf al zouden weten dat de apparaten afkomstig zijn van Electronics? En als vast zou staan dat ze van Phitronics zijn?

Vraag b
Hoe groot is de kans op twee defecten als we niet weten wie de leverancier was?

Vraag c
Gegeven het feit dat we twee defecte apparaten vonden in een steekproef van 20, hoe groot is de kans dat Phitronics de leverancier is van deze partij? (hint; regel van Bayes)

Bron "Statistiek om mee te werken", (9e druk) van Prof.dr. Arie Buijs.

edward
Student hbo - zondag 1 mei 2016

Antwoord

Hallo Edward,

We hebben onderling flink gediscussieerd over mogelijke andere interpretaties van jouw vragen, maar we komen tot de conclusie dat de door jou gegeven antwoorden (deels) onjuist zijn. De juiste uitwerking is:

Vraag a)
De kans op een defect bij Electronics is 0,1. Het aantal defecten binnen een steekproef van 20 stuks is dan binomiaal verdeeld. De kans op precies 2 defecten bij Electronics is:



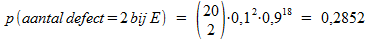
Op dezelfde wijze vinden we de kans op twee defecten bij Phitronics:



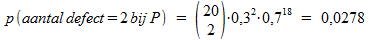
Vraag b)
60% van de apparaten is afkomstig van Electronics, waarvan 10% defect is. 40% is afkomstig van Phitronics, waarvan 30% defect is. Het totale percentage defecte apparaten is dan:
10% van 60% + 30% van 40% = 6% + 12% = 18%

Ofwel: de kans dat een willekeurig apparaat uit de gehele voorraad defect is, is 0,18.
Het aantal defecten binnen een steekproef van 20 apparaten uit de gehele voorraad is opnieuw binomiaal verdeeld. De kans op precies 2 defecten is:



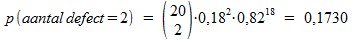
(Zie aanvulling onderaan)

Vraag c)



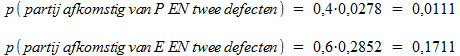
Hiermee vinden we:



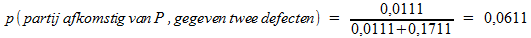
Aanvulling vraag b:
Wellicht moet deze vraag gelezen worden als: een gehele partij is afkomstig van één leverancier, 40% kans dat de partij afkomstig is van Phitronics, 60% kans dat deze partij afkomstig is van Electronics. Uit deze partij wordt de steekproef getrokken.
In dat geval bereken je de kans op twee defecten met:

p(2 defecten) = 0,4·0,0278 + 0,6·0,2852 = 0,1822

Deze partij moet dan wel zo groot zijn dat de kans op een defect apparaat niet verandert wanneer exemplaren voor de steekproef uit de partij worden gehaald (ofwel: het trekken zonder terugleggen mag worden benaderd door trekken met terugleggen).

vrijdag 6 mei 2016

Re: Afgekeurde koffiezetters

©2001-2024 WisFaq