
Gelijke cirkelverdeling
Geacht heer/ mevrouw,
Hoe verdeel ik een cirkel verticaal in 3 gelijke stukken qua oppervlakte? Bijvoorbeeld vanuit het midden is het makkelijk: je meet gewoon 120 graden iedere keer. Maar hoe bepaal je dit verticaal?
Bij voorbaat dank.
Martin
Ouder - vrijdag 6 maart 2015
Antwoord
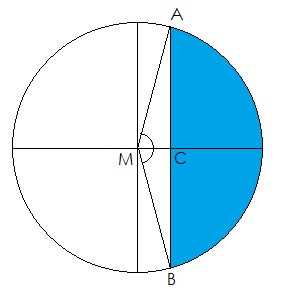
We zoeken de afstand van M (middelpunt) tot C zodat de oppervlakte van het rechter (blauwe) segment gelijk is aan 1/3 van de oppervlakte van de cirkel.
De oppervlakte van een cirkelsegment =
r2/2.(q - sin q) met q = hoek AMB.
Dus :
r2/2.(q - sin q) = 1/3.pr2
of
q - sin q = 2p/3
Deze vergelijking is grafisch op te lossen door de grafiek y = x - sinx te laten snijden de horizontale rechte y = 2p/3
Je vindt dan dat x = q = 2,60533 rad
De hoek AMC is dan 1,30267 rad = 74,637°
In de rechthoekige driehoek AMC vind je dan dat |MC| = |AM|.cos(74,637°) = r.cos(74.637°) = 0,26493.r

vrijdag 6 maart 2015
 ©2001-2024 WisFaq
©2001-2024 WisFaq
|