Wedstrijd uitslag met meerdere variabelen

Ik ben door mijn vereniging gevraagd om voor het volgende probleem een excel-bestand in elkaar te knutselen.

Ik ben lid van een schutterij. Onze schutterij wil dit jaar deelnemen aan een schuttersevenement, het Kinder-OLS. De Limburgse schutters federatie heeft scholen uitgenodigd, om met ondersteuning van de plaatselijke schutterij, deel te nemen aan het Kinder-OLS. Dit betreft het nabootsen van een schuttersfeest door de schoolkinderen, om zo met dit cultuur-historisch erfgoed in contact te komen.

Een van de onderdelen hiervoor, is het schieten met een luchtgeweer. De kinderen moeten hiervoor oefenen, en uiteindelijk mogen de beste schutters aan het wedstrijd-zestal deelnemen.

Het probleem dat zich nu voordoet: omdat dit geheel op vrijwillige basis gebeurt, zijn de kinderen niet verplicht tot een bepaalde deelname aan de oefenwedstrijden. In totaal hebben we ca. 10 oefenwedstrijden. Per oefenwedstrijd is het aantal schoten dat ze kunnen schieten ook niet vast te leggen, omdat dit afhankelijk is van het aantal kinderen dat bij die oefenwedstrijd aanwezig is.

In het verleden hebben we de kwaliteit van de schutters proberen vast te stellen door van het aantal schoten en het aantal gescoorde punten een percentage vast te stellen. Dit gaf enige indicatie, maar het probleem hierbij is, dat als een kind 1 schot doet, en dit is ook nog raak, hij een score van 100% haalt. Een kind dat 500 schoten doet en 5 missers heeft, scoort dan minder. Wat ik nu zoek is een wiskundige berekening die rekening kan houden met het totaal aantal schoten, het aantal gescoorde punten, het aantal gehouden oefeningen en het aantal deelgenomen oefeningen.

Wie kan mij hiermee helpen?

jan th
Leerling mbo - maandag 26 mei 2014

Antwoord

Beste Jan,

Als ik jouw vraag goed begrijp, wil je uit de score van elke schutter zo goed mogelijk de werkelijke trefkans bepalen. Zoals je zelf al aangeeft, kan je deze kans niet met zekerheid vaststellen omdat toeval ook een rol speelt. Wanneer iemand 6 uit 10 scoort, is de beste schatting van de trefkans natuurlijk 0,6 (=60%), maar misschien is de werkelijke trefkans wel 0,5 en heeft deze schutter een beetje geluk gehad (of juist 0,7 en heeft de schutter pech gehad).
Een wetenschappelijk volledig verantwoord antwoord zou een half boekwerk vragen, daar zit je vast niet op te wachten. Ik doe een poging om een werkbaar antwoord te geven.

Als voorbeeld neem ik 3 schutters, hieronder staan het aantal treffers en het aantal pogingen:

• Schutter A: 2 uit 3 (67%)
  
• Schutter B: 6 uit 10 (60%)
  
• Schutter C: 50 uit 100 (50%)

Schutter (2 uit 3) heeft de hoogste score, maar tegelijkertijd is het risico van vertekening door een toevalstreffer het hoogst.
Onderstaande grafiek geeft het verband weer tussen de minimale trefkans die je aan een schutter toekent, en het risico dat je hiermee fout zit (op de berekeningen kom ik terug):



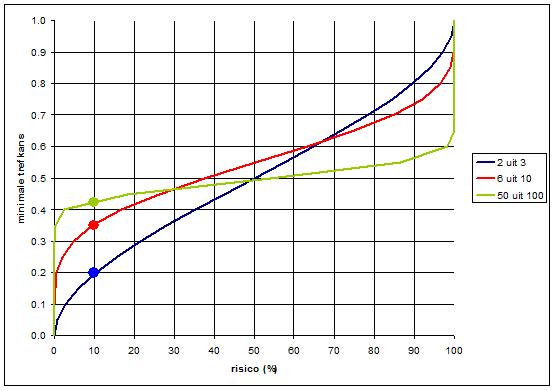
De grafiek kan je als volgt gebruiken:

Stel je wilt de minimale trefkans bepalen met weinig risico op een onjuiste conclusie (risico=10%, een voorzichtige schatting). In de grafiek lees je af:

• schutter (2 uit 3): minimale trefkans = 0,20 (zie blauwe punt)
  
• schutter (6 uit 10): minimale trefkans = 0,36
  
• schutter (50 uit 100): minimale trefkans = 0,42

Bij deze voorzichtige schatting (risico=10%) selecteer je schutter (50 uit 100). Je weet redelijk zeker dat jouw deelnemer een score van minimaal 0,42 haalt.

Bij risico=40% ligt de rode lijn het hoogst, op 0,51. Ben je bereid dit risico te nemen, dan selecteer je schutter (6 uit 10) omdat je hiermee de hoogste trefkans kiest. Maar je loopt een risico van 40% dat deze conclusie onjuist is.

Ben je bereid veel risico te lopen (80%), dan selecteer je schutter (2 uit 3). Als zijn oefeningen representatief zijn, dan heb je een schutter met minimale trefkans=0,71 geselecteerd. Maar je loopt 80% risico dat deze schutter in werkelijkheid tegenvalt.

Samengevat komt het neer op het volgende: hoe meer pogingen een schutter heeft gedaan, hoe vlakker de lijn loopt. Uiteindelijk geeft de lijn de werkelijke trefkans weer.
Bij weinig pogingen kantelt de lijn: de linkerkant zakt, en daarmee zakt de schatting van de werkelijke trefkans. Dit kan je zien als een veiligheidsmarge. De rechterkant gaat juist omhoog: een schutter kan ook een keer 'te veel' hebben gemist. De werkelijke trefkans is dan hoger dan de score. Je kunt hierop gokken, maar je neemt dan veel risico.

Op de een of andere manier moet je een keuze maken voor het risiconiveau. Bij een laag risico zal je eerder een schutter selecteren die veel pogingen heeft gedaan. Ook al heeft hij een wat lagere score, je weet wat je aan hem hebt en de kans op een uitschieter naar beneden (maar ook naar boven!) is niet zo groot.
Bij een hoog risico geef je eerder het voordeel van de twijfel aan een schutter die minder heeft geoefend, maar wel succesvol was. Je hoopt dat dit geen toeval was, dan zal de score bij de wedstrijden hoog zijn. Maar als het succes bij het oefenen wel geluk is geweest, dan vallen de wedstrijden tegen. Je weet niet goed wat je aan hem hebt, je neemt een gok.
In mijn ogen kan van gemotiveerde deelnemers worden verwacht dat zij voldoende oefenen. De keuze voor een laag risico kan wellicht een stimulans zijn om voldoende te oefenen.

Nu de berekeningen achter de grafieken:
Wanneer iemand 6 uit 10 scoort, bereken ik voor alle trefkansen tussen 0 en 1 de kans dat bij 10 pogingen minstens 6 treffers zitten. Bijvoorbeeld:
Trefkans=0,4: kans op (aantal raak minstens 6)=0,17. Wanneer een schutter deze score heeft, is er een risico van 17% dat zijn werkelijke trefkans 0,4 of minder is.

In Excel (Nederlandse versie) maak je deze formule:
p=trefkans (in mijn voorbeeld: 0,4)
n=aantal pogingen (in mijn voorbeeld: 10)
k=aantal treffers (in mijn voorbeeld: 6)
risico = =(1-BINOMIALE.VERD(k-1;n;p,ONWAAR))*100

Voer deze berekening uit voor p=0 t/m p=1. De waarde van p bij de door jou gekozen waarde voor risico is de schatting van de minimale trefkans voor deze schutter. Selecteer vervolgens de schutters met de hoogste minimale trefkansen.

Hopelijk kan je met dit antwoord vooruit. Reageer gerust als je nog vragen hebt.

vrijdag 30 mei 2014

©2001-2024 WisFaq