De oppervlakte van G berekenen

Voor x element van [0,$\pi$] zijn de functies gegeven:

f(x)=tan²x (x niet gelijk aan $\frac{\pi}{2}$)
g(x)=4sin²x

l is de rechte met als vergelijking $\frac{3\pi}{4}$. G is het vlakdeel rechts van l, begrensd door l, en de grafieken f en g.

• Bereken exact de oppervlakte van G.

Ik ben begonnen de snijpunten te berekenen maar daarna weet ik niet meer hoe ik mijn integraal moet opstellen.

Vandev
3de graad ASO - zondag 16 februari 2014

Antwoord

Een tekening?



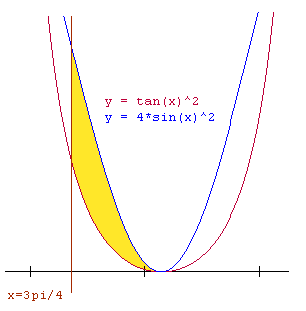
Je krijgt dan:

$
\int\limits_{\frac{{3\pi }}{4}}^\pi {4\sin ^2 (x) - \tan ^2 (x)\,dx}
$

Ben je er dan?

zondag 16 februari 2014

Re: De oppervlakte van G berekenen

©2001-2024 WisFaq