Afgeleide (sec x) (1 en tan x)

Beste wiskunde knobbels,

Ik moet de afgeleide f(x) = (sec x) / (1 + tan x) berekenen.
Nu loop ik vast op dit punt:

f'(x) = sec( tan(x) + tan²(x) - sec²(x) )
---------------------------------
(1 + tan(x))²

Het antwoord is:
f'(x) = sec(x) ( tan x - 1 )
---------------------------------
(1 + tan(x))²

Ik mis de laatste paar stappen volgens mij, want ik kom hier niet uit.
Hoe kan sec( tan(x) + tan²(x) - sec²(x) ) gelijk zijn aan sec(x) ( tan x - 1 )

Alvast bedankt voor uw antwoord :)

Groetjes

Ben

Ben
Student hbo - zaterdag 9 juli 2011

Antwoord

Dag Ben,

Het antwoord op jou vraag luidt: Dat kan niet gelijk zijn aan elkaar, want het is niet gelijk aan elkaar. Ik snap ook niet dat je bij de teller een hele rits van goniometrische formules IN de sec-formule hebt gekregen. Daar gaat dus ergens iets fout, maar ik weet niet waar het bij jou fout gaat. Ik zou het in ieder geval als volgt oplossen:



Vervolgens nog even vereenvoudigen tot de gewenste oplossing:



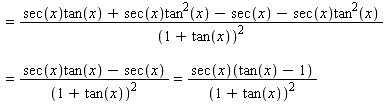
Mvg Thijs Bouten

zaterdag 9 juli 2011

Re: Afgeleide (sec x) (1 en tan x)

©2001-2024 WisFaq