Onbetrouwbaarheid

Een groep van 400 studenten is aan het einde van het eerste studiejaar gevraagd of zij tevreden zijn over hun studiekeuze. Als oordeel zijn drie antwoorden mogelijk: enthousiast, onverschillig, teleeurgesteld. Verder zijn de antwoorden verdeeld naar studierichting: BE, CE, BSK en EL. De resultaten staan in de volgende tabel:


Oordeel Studierichting
BE CE BSK EL Totaal

Enthousiast 50 30 40 30 150
Onverschillig 5 35 15 105 160
Teleurgesteld 25 15 5 45 90

Totaal 80 80 60 180 400


a. Toets met onbetrouwbaarheid á = 0.01 of de oordelen samenhangen vertonen met de gekozen studierichting.
b. Wat zou het gevolg zijn van een grotere betrouwbaarheid bij deze gegevens?

willia
Student Hoger Onderwijs België - woensdag 4 december 2002

Antwoord

De waargenomen (Observed) en verwachte (Expected) frequenties staan hieronder:



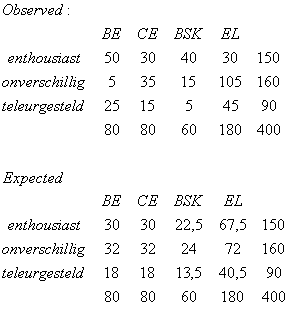
De Expected frequenties bereken je als volgt.
De nulhypothese is dat de beoordeling van de studie onafhankelijk is van de studiekeuze.
In dat geval verwacht je dat studenten van elke richting verhoudingsgewijs even vaak enthousiast, onverschillig en teleurgesteld moeten zijn.
In totaal zijn 150 van de 400 studenten enthousiast. Er zijn in totaal 80 studenten BE dus als hun studiekeuze niet van invloed zou zijn, verwacht je 150/400*80=30 enthousiaste BE studenten. Net zo verwacht je 160/400*80=32 onverschillige BE studenten en 90/140*80=18 teleurgestelde BE studenten.
Op dezelfde manier bereken je de verwachte frequenties voor de andere studierichtingen.

Nu is de vraag of je waargenomen frequenties (Observed) zo sterk afwijken van de verwachte frequenties dat de aanname dat de studierichting er niet toe doet nog houdbaar is.

Hiervoor bereken je de grootheid chi-kwadraat.
Zoek in je leerboek op hoe deze wordt berekend.
De uitkomst is:
chi-kwadraat = 98.41.
Het aantal vrijheidsgraden df = (aantal rijen - 1)x(aantal kolommen - 1) = 2 x 3 = 6.
Kijk nu in de chi-kwadraat tabel.
De overschrijdingskans is bijzonder klein (5.37 ·10^-19), in ieder geval kleiner dan 0,01.
De kans dat je deze frequenties waarneemt terwijl de beoordeling onafhankelijk zou zijn van de gekozen studie, is dus bijzonder klein. Je verwerpt dus deze (nul)hypothese.

b) Hier begrijp ik de vraagstelling niet. Wat bedoelen ze met grotere betrouwbaarheid bij de gegevens?

woensdag 4 december 2002

©2001-2024 WisFaq